---

一、前言

AcWing算法提高课内容，本文讲解 动态规划 第一讲：数学三角形模型

本篇包括以下题目：
AcWing 1015. 摘花生
AcWing 1018. 最低通行费
AcWing 1027. 方格取数
AcWing 275. 传纸条

写博客有哪里不完善的地方或者有哪里表达错误希望大家提出来，博主会立即改正！望大家海涵

---

二、AcWing 1015. 摘花生

1.题目

本题链接：摘花生
本博客提供本题截图：

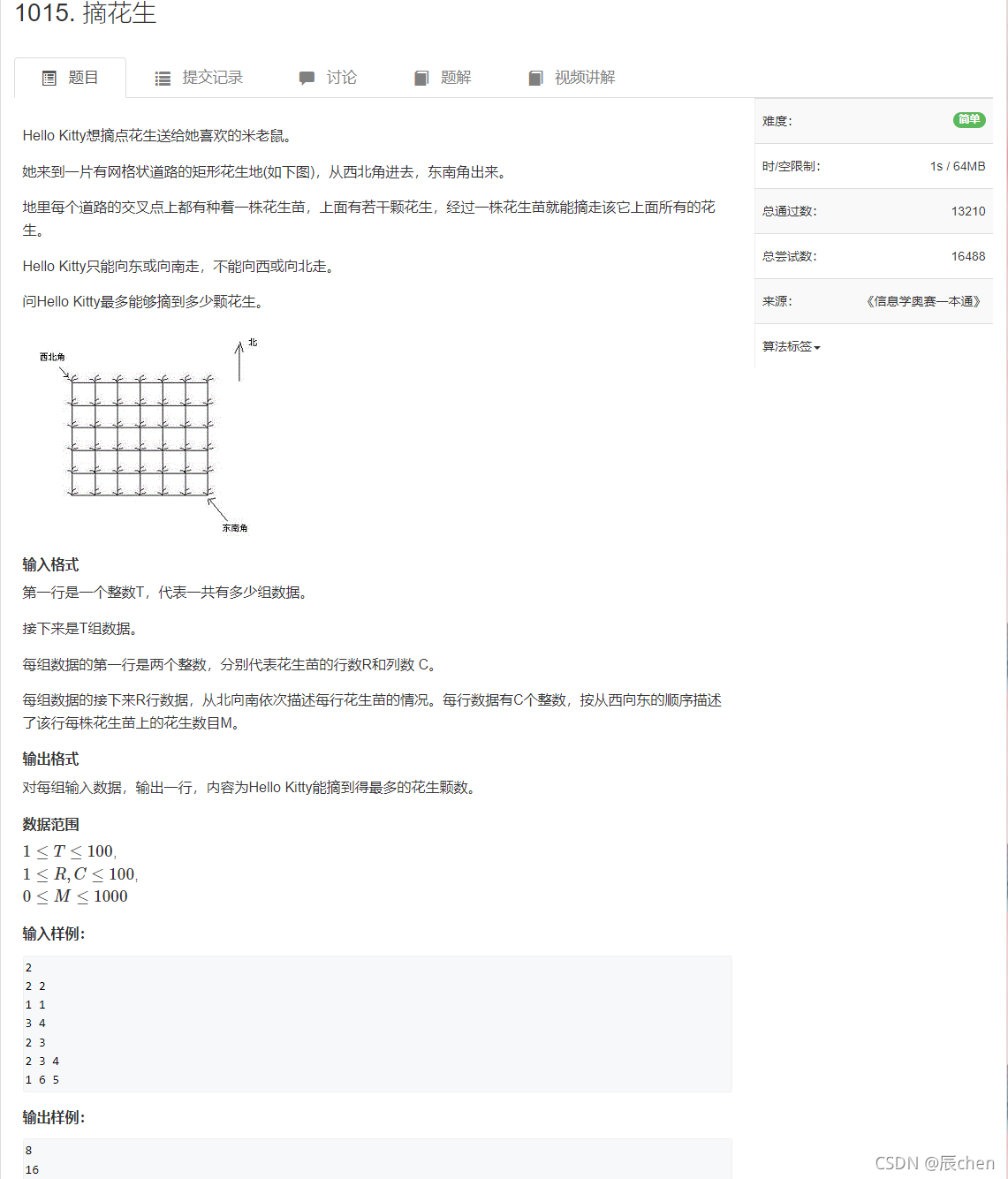
2.逻辑解释

拿到一个题目后，我们分为两步去考虑这个问题：
第一步： 把题目进行抽象：其实就是对于一个矩形，我们从它的左上角走到右下角，每一个点上都一个数值，走到一个点后就加上这个点的值，每次只能往右走或者往下走，问走到右下角的话，数值的累计最大值是多少。
第二步： 进行dp分析：比如我们现在在[i, j]这个点上，dp的关键就是分析这个点可以由哪个点转换而来：显然，对于这个点而言，根据题意可以由上面的一个点转换，亦可由左边的一个点转换过来，而我们的需求为最大值，故我们可以得到状态转移方程：

f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j];

3.AC代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int w[N][N];
int f[N][N];

int main()
{
    int t;
    cin >> t;
    
    while (t -- ) 
    {
        int r, c;
        cin >> r >> c;
        for (int i = 1; i <= r; i ++ ) 
            for (int j = 1; j <= c; j ++ ) 
                cin >> w[i][j];
                
        for (int i = 1; i <= r; i ++ ) 
            for (int j = 1; j <= c; j ++ )
                f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j];
                
        cout << f[r][c] << endl;
    }
    
    return 0;
}

---

三、AcWing 1018. 最低通行费

1.题目

本题链接：最低通行费
本博客提供本题截图：

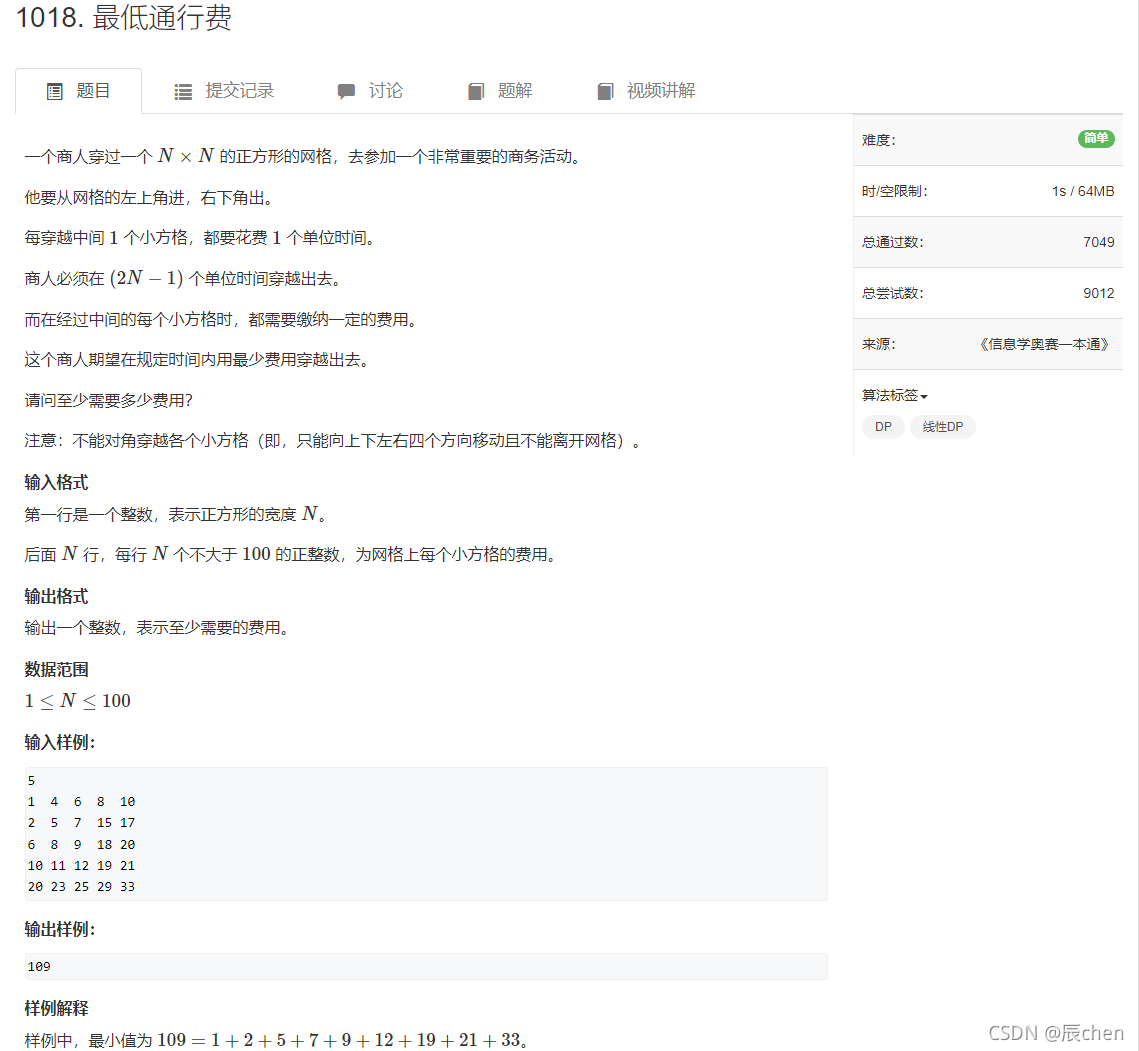
2.逻辑解释

拿到一个题目后，我们分为两步去考虑这个问题：
第一步： 把题目进行抽象：其实就是对于一个矩形，我们从它的左上角走到右下角，每一个点上都一个数值，走到一个点后就加上这个点的值，每次只能往右走或者往下走，问走到右下角的话，数值的累计最小值是多少。
第二步： 进行dp分析：比如我们现在在[i, j]这个点上，dp的关键就是分析这个点可以由哪个点转换而来：显然，对于这个点而言，根据题意可以由上面的一个点转换，亦可由左边的一个点转换过来，这里或许你会考虑：那么边界情况是否需要我们特判呢？即当我们的i或者j等于1的时候，需要特判，这个题和上一个题的区别就有了，因为我们的数组是从下标1开始的，而因为我们数组为全局定义，i = 0和j = 0的点的值是默认为0的，而我们的需求为最小值，故我们需要去特判，故我们可以得到状态转移方程：

if (i != 1 && j != 1)
	f[i][j] = min(f[i - 1][j], f[i][j - 1]) + w[i][j];
else if (i == 1) f[i][j] = f[i][j - 1] + w[i][j];
else f[i][j] = f[i - 1][j] + w[i][j];

3.AC代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int w[N][N];
int f[N][N];

int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i ++ ) 
        for (int j = 1; j <= n; j ++ ) 
            cin >> w[i][j];
            
    for (int i = 1; i <= n; i ++ ) 
        for (int j = 1; j <= n; j ++ ) 
            if (i != 1 && j != 1)
                f[i][j] = min(f[i - 1][j], f[i][j - 1]) + w[i][j];
            else if (i == 1) f[i][j] = f[i][j - 1] + w[i][j];
            else f[i][j] = f[i - 1][j] + w[i][j];
            
    cout << f[n][n] << endl;
    
    return 0;
}

---

四、AcWing 1027. 方格取数

1.题目

本题链接：方格取数
本博客提供本题截图：

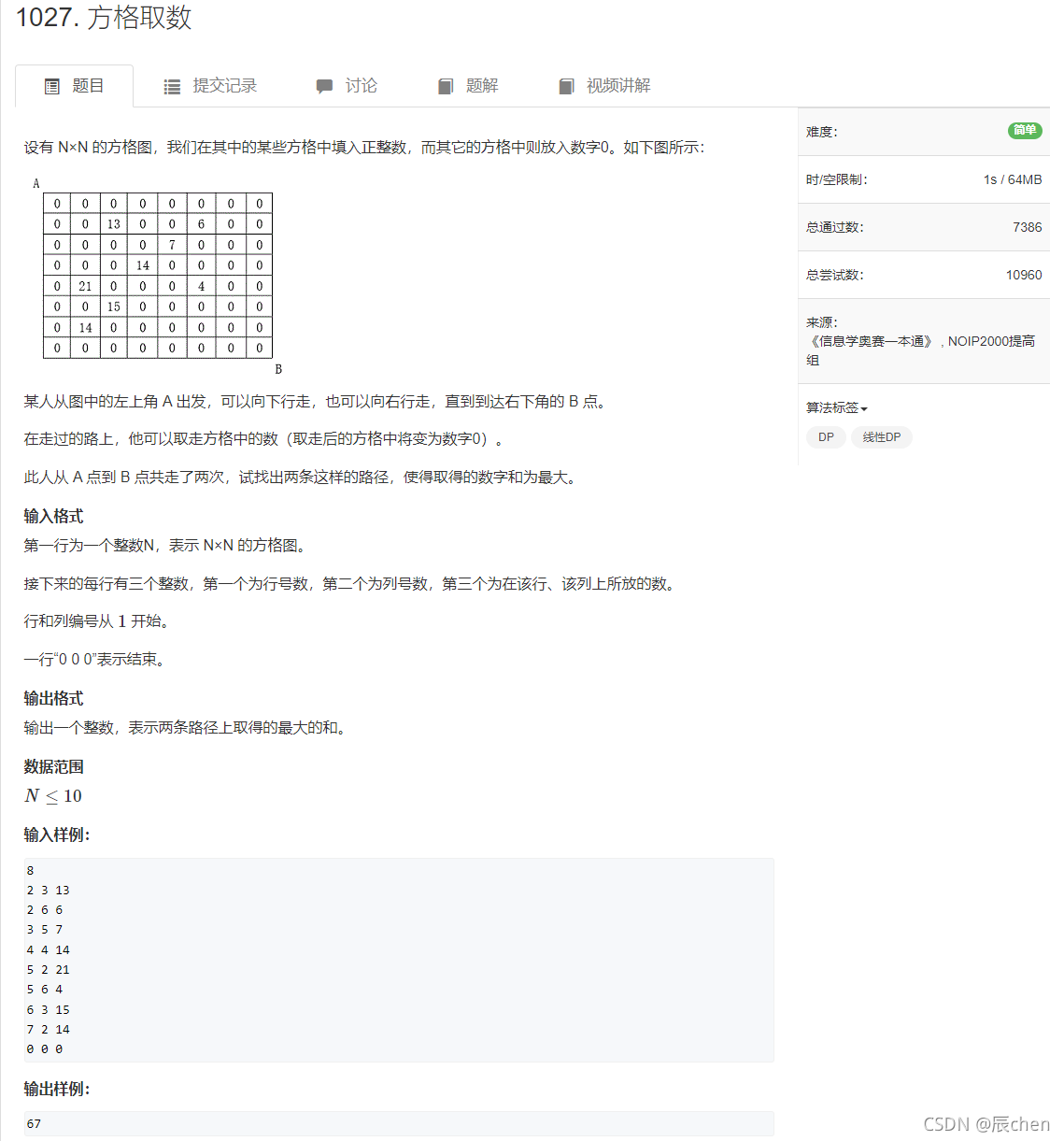
2.逻辑解释

这个题其实可以看成是第一题的升级版，我们可以如此抽象这道题目：有两个人按照一题中的规则同时进行移动，问两个人到达右下角后最大的和，我们引入变量k = i1 + j1 = i2 + j2，其中k代表走的步数和，i1, j1代表第一个人的位置，因为每一次只能移动一个格子，所以走的总步数就是i1 + j1，第二个人同理，由于我们规定这两个人是同时开始移动，故有k = i1 + j1 = i2 + j2，本题中，需要判断两个人走的是否为同一个格子，即(i1,j1),(i2,j2)是否为用一个点，如果是同一个点，则需要加一次值，否则需要加两个格子上的值

3.AC代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 15;

int f[2 * N][N][N];
int w[N][N];

int main()
{
    int n;
    cin >> n;
    int a, b, c;
    while (cin >> a >> b >> c, a || b || c)
        w[a][b] = c;
        
    for (int k = 2; k <= 2 * n; k ++ ) 
        for (int i1 = 1; i1 <= n; i1 ++ ) 
            for (int i2 = 1; i2 <= n; i2 ++ )
            {
                int j1 = k - i1, j2 = k - i2;
                if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)   //不能越界
                {
                    int &x = f[k][i1][i2];
                    int t = w[i1][j1];
                    if (i1 != i2) t += w[i2][j2];
                    x = max(x, f[k - 1][i1 - 1][i2 - 1] + t); //都是从上往下走
                    x = max(x, f[k - 1][i1][i2] + t);   //都是从左往右走
                    x = max(x, f[k - 1][i1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1 - 1][i2] + t);
                }
            }
            
    cout << f[2 * n][n][n] << endl;
    
    return 0;
}

---

五、AcWing 275. 传纸条

1.题目

本题链接：传纸条
本博客提供本题截图：

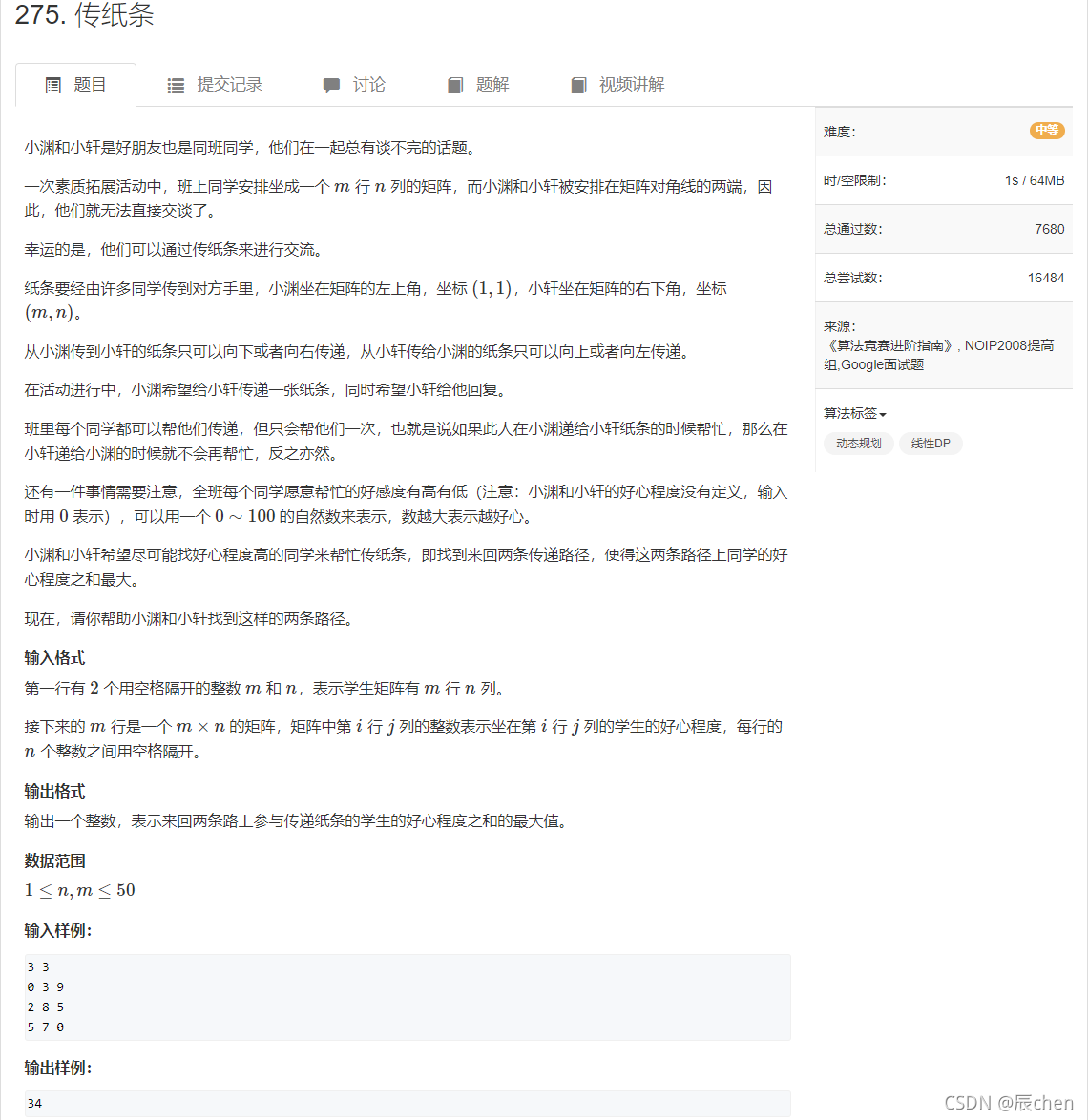
2.逻辑解释

这个题我们是特殊规定了不可以有交集，那么入手点其实就是在交集上，我们先来判断如果有交集该怎么处理：
我们还是沿用上一题的思路，看成两个人从矩阵的左上角走到右下角，这两个人是同时走一步，且两个人不能有路径重合。
因为我们规定了这两个人是同时出发每次同时走一格，故我们路径中相遇的地方一定是同时走到的（注意只有最左上角的点(初始点)和最右下角(结束点)是可以被两次走过的，其他的点都仅可走一次）
状态表示：f[k, i1, i2]表示两个人同时走了k步，第一个人此时位于(i1, k - i1)处，第二个人此时位于(i2, k - i2)处的所有走法的最大值。
两个人同时往右走：f[k - 1, i, j] + mark[k, i, j];
两个人同时往下走：f[k - 1, i - 1, j - 1] + mark[k, i, j];
第一个人往右走第二个人往下走：f[k - 1, i, j - 1] + mark[k, i, j];
第一个人往下走第二个人往右走：f[k - 1, i - 1, j] + mark[k, i, j];

3.AC代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 55;

int g[N][N];
int f[2 * N][N][N];
int n, m;

int main()
{
    cin >> m >> n;
    for (int i = 1; i <= m; i ++ ) 
        for (int j = 1; j <= n; j ++ ) 
            cin >> g[i][j];
            
    for (int k = 2; k <= n + m; k ++ ) 
        for (int i = max(k - n, 1); i <= min(k - 1, m); i ++ ) 
            for (int j = max(k - n, 1); j <= min(k - 1, m); j ++ ) 
            {
                if ((i == j) && (k != 2) && (k != n + m)) continue;
                int w = g[i][k - i] + g[j][k - j];
                for (int a = 0; a <= 1; a ++ )
                    for (int b = 0; b <= 1; b ++ ) 
                        f[k][i][j] = max(f[k][i][j], f[k - 1][i - a][j - b] + w);
            }
            
    cout << f[n + m][m][m] << endl;
    
    return 0;
}

---