《异常检测——从经典算法到深度学习》

• 0 概论
• 1 基于隔离森林的异常检测算法
• 2 基于LOF的异常检测算法
• 3 基于One-Class SVM的异常检测算法
• 4 基于高斯概率密度异常检测算法
• 5 Opprentice——异常检测经典算法最终篇
• 6 基于重构概率的 VAE 异常检测
• 7 基于条件VAE异常检测
• 8 Donut: 基于 VAE 的 Web 应用周期性 KPI 无监督异常检测
• 9 异常检测资料汇总（持续更新&抛砖引玉）
• 10 Bagel: 基于条件 VAE 的鲁棒无监督KPI异常检测
• 11 ADS: 针对大量出现的KPI流快速部署异常检测模型
• 12 Buzz: 对复杂 KPI 基于VAE对抗训练的非监督异常检测
• 13 MAD: 基于GANs的时间序列数据多元异常检测
• 14 对于流数据基于 RRCF 的异常检测

相关：

• VAE 模型基本原理简单介绍
• GAN 数学原理简单介绍以及代码实践

14. 对于流数据基于 RRCF 的异常检测

2016 Robust random cut forest based anomaly detection on streams
论文下载以及源码地址 github
论文发表于 ICML会议（International Conference on Machine Learning）CCF A
RRCF 的实现论文 下载地址
翻译部分请前去我的个人博客：smileyan.cn

14.1 简要概述论文内容

14.1.1 核心思想与方法

随机森林(Random Forest, RF) 是一种 bagging 算法，这篇论文提到的 RRCF (Robust Random Cut Forest) 是在 RF 的基础上进行改进的，以达到"健壮"的效果。所以这篇论文的核心思想就是，改进 RF 成为 RRCF ，定义与证明一些 RRCF 的性质，并且实验证明 RRCF 的效果。

所以整篇论文应该包括以下几方面内容：

• 什么是RRCF？
• RRCF 相对于 RF 改进之处在哪，怎么改进的？
• RRCF 是如何应用在流数据（即时间序列数据）的异常检测的。

因为定义比较多，我们也将一个一个地往下看。

14.1.2 RRCF 的生成过程

首先了解一下RF的生成过程，这对于继续了解RRCF很有帮助。

集成方法的目标是将多个基本估计器的预测与给定的学习算法相结合，以提高单个分类器的通用性/鲁棒性。集成方法包括两种：Boosting 和 bagging。随机森林是bagging的典型代表。

随机森林的生成过程是可以并行的，也就是说，

• 每棵树的生成是互不相干的；
• 每棵树生成对应的数据的采样也是互不相关的（有放回地随机采样）
• 每棵树的地位都是相等的，这个与boosting思想差别很大。

接着具体到每个树的生成，这与决策树的构建步骤没什么区别。而决策树的生成过程容易理解，参考找工作过程基本上就明白了，首先工资不能低于多少，分为两类，接着年终不低于多少钱，继续分两类等等。

接下来关注 RRCF 的生成过程，也就是论文中的 定义1：

定义1（Definition 1 ） 对于点集$S$，一棵健壮随机分割树以如下方式生成：

1. 选择一个与 $\frac{{\ell }_i}{{\sum }_j{\ell }_j}$ 成比例的随机维度，其中 ${\ell }_i=ma{x}_{x\in S}{x}_i-mi{n}_{x\in S}{x}_i$。
2. 选一个 $X_i\sim Uniform[mi{n}_{x\in S}{x}_i,ma{x}_{x\in S}{x}_i]$ 也就是从最小到最大的均匀分布。
3. 设 S 1 = { x ∣ x ∈ S , x i ≤ X i } S_1=\{x|x\in S,x_i\le X_i\} S1​={x∣x∈S,xi​≤Xi​}​​​​​ ，$S_2=S{S}_1$​​​​​ 和 基于 $S_1$ 与 $S_2$ 的递归。

与之相关的 定理1

定理 1（Theorem 1）

考虑定义 1 中的算法。让树中节点的权重为相应的维数之和 ${\sum }_i{\ell }_i$。给定两个点 $u,v\in S$，将 $u$ 和 $v$ 之间的树距离定义为 $u,v$ 的最小公共祖先的权重。那么，树的距离最小是曼哈顿距离（Manhattan distance）$L_1(u,v)$ ，最大距离是 $O(d\log \frac{|S|}{L_1(u,v)})\ast L_1(u,v)$。

14.1.3 RRCF 的分割过程

定理 2（Theorem 2）

给定一棵根据 $\mathcal{T}(S)$​ 生成的树，如果我们删除包含孤立点 $x$​ 以及其父节点（相应地调整祖辈点，如 图2 所示），则生成的树 $T^{\prime }$​ 的概率与 T ( S − { x } ) \mathcal{T}(S-\{x\}) T(S−{x})​ 中生成的概率相同。 同样，我们可以生成一棵树 $T^{\prime \prime }$​ 就像从 T ( S   ∪ { x } ) T(S\ \cup \{x\}) T(S ∪{x}) ​随机抽取一样，当最大深度为 $T$ 时它的生成时间复杂度为 $O(d)$ ，这通常是 $|T|$ 中次线性 (sublinear) 的。

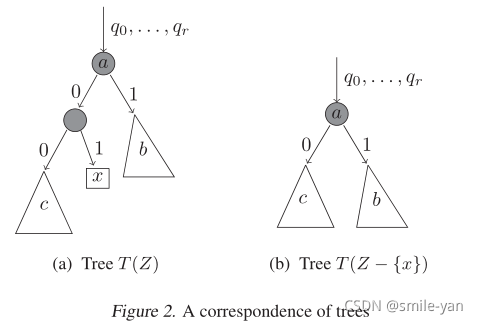
这个是可以理解的，切割后的剩下的 $c$ 就代表了之前它的整个父节点，自然不会发生概率变化。

接下来的 定理3， 定理4， 定理5 稍微看一下即可，性能方面的一些考量。

14.1.4 定义异常

首先论文举了个例子，某个人戴帽子换颜色的例子，说实话这个例子不怎么好。

定义2

将点 $x$ 的位移（bit-displacement）或移动（displacement）定义为所有其他点的模型复杂度的增加，即，对于集合 $Z$ ，要捕获 $x$ 的外部性（离群性），定义
D I S P ( x , Z ) = ∑ T , y ∈ Z − { x } P r [ T ] ( f ( y , Z , T ) − f ( y , Z − { x } , T ′ ) ) DISP(x, Z)=\sum_{T, y\in Z-\{x\}} \mathbb{P}r[T](f(y,Z,T)-f(y,Z-\{x\},T')) DISP(x,Z)=T,y∈Z−{x}∑​Pr[T](f(y,Z,T)−f(y,Z−{x},T′))
其中 T ′ = T ( Z − { x } ) T'=T(Z-\{x\}) T′=T(Z−{x}) 。

1The converse is not true, this is a many-to-one mapping.

反过来不成立，这个是多对一映射。

14.1.5 基于流的森林维护

插入(Insertion)： 给定从 $RRCF(S)$ 分布中抽取的样本 $T$ 和点 $p\notin S$，从 R R C F ( S ∪ { p } ) RRCF(S\cup \{p\}) RRCF(S∪{p}) 分布中抽取得到样本 $T^{\prime }$。

检测(detection): 给定从 $RRCF(S)$ 分布中抽取的样本 $T$ 和点 $p\in S$，从 R R C F ( S ∪ { p } ) RRCF(S\cup \{p\}) RRCF(S∪{p}) 分布中抽取得到样本 $T^{\prime }$。我们需要进行以下简单的观察。

观测1(Observation 1 ) 当且仅当可以使用轴平行切割分离最小轴对齐边界框 $B(S)$ 和 $p$ 时，才可以使用轴平行切割分离点集 $S$ 和 $p$ 。

下一个引理提供了关于RRCF树的结构属性。我们对增量更新感兴趣，对一组树进行尽可能少的更改。请注意，给定一个特定的树，我们有两种详尽的情况，（i）要删除（分别插入）的新点不被第一个切割分开，（ii）要删除（分别插入）的新点被第一个切割分开。引理3针对分别满足（i）和（ii）的树集合（不仅仅是一棵树）解决了这些问题

引理 3 (Lemma 3)

给定点 $p$ 和一组点 $S$，其轴平行于最小边界框 $B(S)$，使得 $p\notin B$:

• 对于任何维度 $i$ ，使用加权隔离林算法选择维度 $i$ 中分裂的轴平行切割的概率与选择分裂的轴平行切割的条件概率完全相同 S ∪ { p } S\cup \{p\} S∪{p}​ ，条件是不将 $p$ 与 $S$ 的所有点隔离。
• 给定 $RRCF(S)$ 的随机树 S ∪ { p } S\cup \{p\} S∪{p} ，条件是第一次切割将 $p$ 与 $S$ 的所有点隔离，树的其余部分是 $RRCF(S)$ 中的随机树。

更多内容参考 smileyan.cn

14.2 动手实验

论文对应的算法源码在 github.com 已有实现，甚至还有比较完备的文档例子 https://klabum.github.io/rrcf/，不妨前去体验一下。

注意关于算法的实现，这里也有一篇简单的介绍论文 前去查看 。

14.2.1 环境安装

确保 python3 的环境，然后输入命令：

$ pip install rrcf

即可安装。

RRCF 依赖包括：

• numpy (>= 1.15)

RRCF 官方提供的例子的依赖包括：

• pandas (>= 0.23)
• scipy (>= 1.2)
• scikit-learn (>= 0.20)
• matplotlib (>= 3.0)

14.2.2 第一个例子

创建一棵树，

import numpy as np
import rrcf

# A (robust) random cut tree can be instantiated from a point set (n x d)
X = np.random.randn(100, 2)
tree = rrcf.RCTree(X)

# A random cut tree can also be instantiated with no points
tree = rrcf.RCTree()

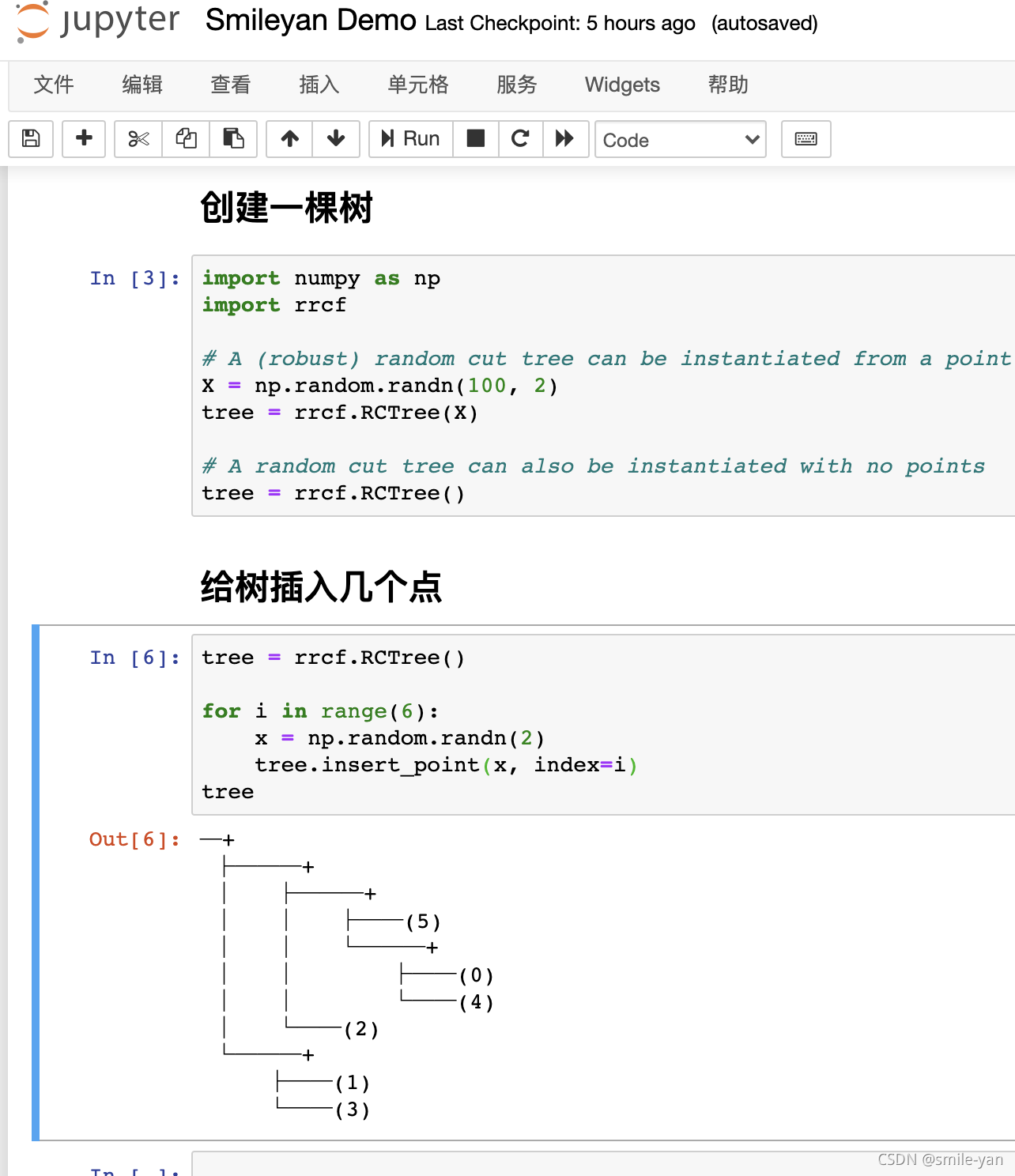
给树插入几个点：

tree = rrcf.RCTree()

for i in range(6):
    x = np.random.randn(2)
    tree.insert_point(x, index=i)
tree

这个时候可以看到如下效果：

删除结点2，

tree.forget_point(2)

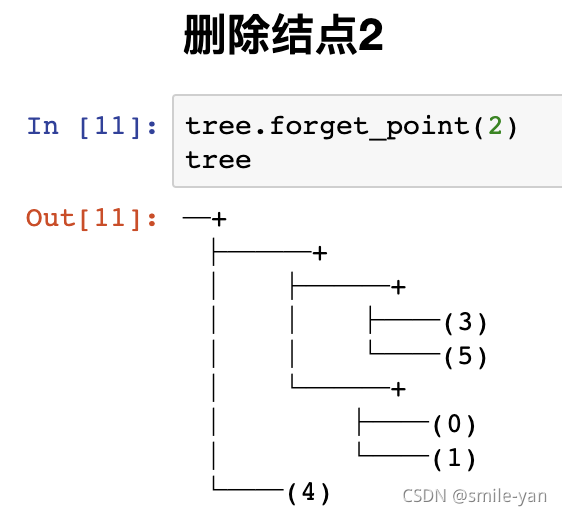
注意这里跟异常检测没关系，只是表示 RRCF 具有这些功能。

14.2.3 RRCF用于异常检测

前面提到过，当插入某个点后，大大增加了模型复杂度，那么这个点极有可能是异常点，这里刚刚有个例子（官方提供）。

# Seed tree with zero-mean, normally distributed data
X = np.random.randn(100,2)
tree = rrcf.RCTree(X)

# Generate an inlier and outlier point
inlier = np.array([0, 0])
outlier = np.array([4, 4])

# Insert into tree
tree.insert_point(inlier, index='inlier')
tree.insert_point(outlier, index='outlier')

代码首先生成正态分布数据作为训练集，这个用来生成数🌲。

接着插入两个点 (0, 0) 和 (4,4) 很明显 （4,4） 不符合正态分布。

最后插入这两个点，附带索引是为了方便查找。

接着看一下插入这两个点给模型带来的复杂度。

tree.codisp('inlier')

tree.codisp('outlier')

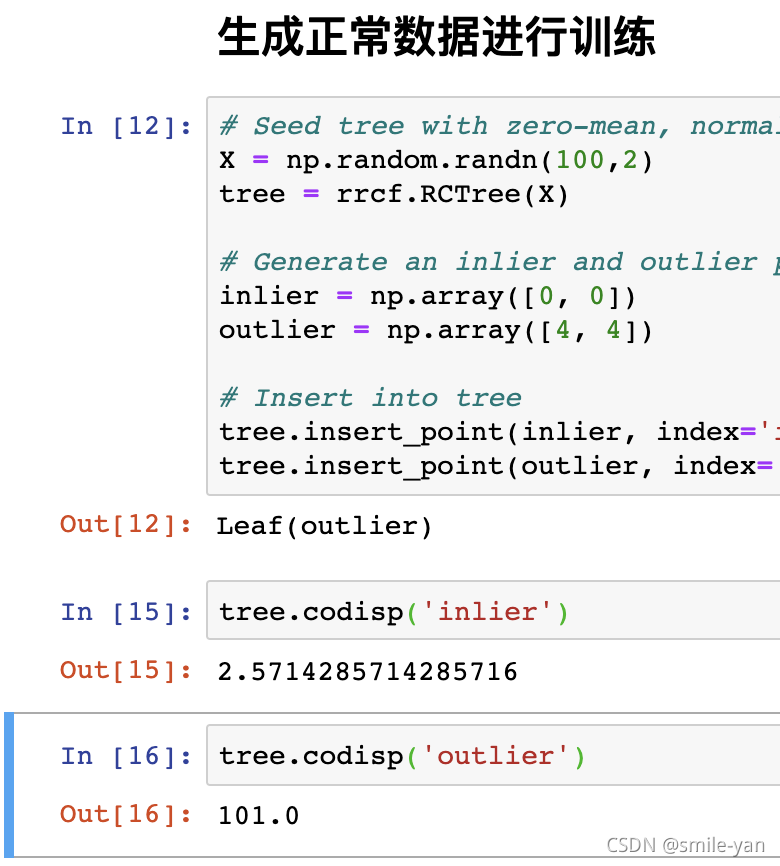
注意由于是随机生成数据，所以结果不一致是非常正常的，不过正常数据输出肯定会比异常数据的输出小很多很多。

14.2.4 RRCF 用于批次异常检测

同样是造数据，但这次是以批次的方式规模较大的进行检测。

import numpy as np
import pandas as pd
import rrcf

# Set sample parameters
np.random.seed(0)
n = 2010
d = 3

# Generate data
X = np.zeros((n, d))
X[:1000,0] = 5
X[1000:2000,0] = -5
X += 0.01*np.random.randn(*X.shape)

# Set forest parameters
num_trees = 100
tree_size = 256
sample_size_range = (n // tree_size, tree_size)

# Construct forest
forest = []
while len(forest) < num_trees:
    # Select random subsets of points uniformly
    ixs = np.random.choice(n, size=sample_size_range,
                           replace=False)
    # Add sampled trees to forest
    trees = [rrcf.RCTree(X[ix], index_labels=ix)
             for ix in ixs]
    forest.extend(trees)

# Compute average CoDisp
avg_codisp = pd.Series(0.0, index=np.arange(n))
index = np.zeros(n)
for tree in forest:
    codisp = pd.Series({leaf : tree.codisp(leaf)
                       for leaf in tree.leaves})
    avg_codisp[codisp.index] += codisp
    np.add.at(index, codisp.index.values, 1)
avg_codisp /= index

计算完成以后，展示一下代码如下：

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import colors

threshold = avg_codisp.nlargest(n=10).min()

fig = plt.figure(figsize=(12,4.5))
ax = fig.add_subplot(121, projection='3d')
sc = ax.scatter(X[:,0], X[:,1], X[:,2],
                c=np.log(avg_codisp.sort_index().values),
                cmap='gnuplot2')
plt.title('log(CoDisp)')
ax = fig.add_subplot(122, projection='3d')
sc = ax.scatter(X[:,0], X[:,1], X[:,2],
                linewidths=0.1, edgecolors='k',
                c=(avg_codisp >= threshold).astype(float),
                cmap='cool')
plt.title('CoDisp above 99.5th percentile')

效果图为：

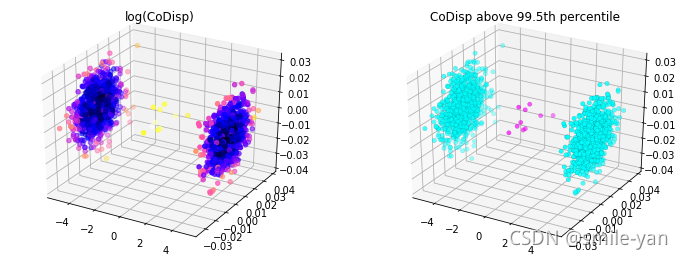
14.2.5 RRCF 用于流数据异常检测

首先生成数据并且进行异常检测

import numpy as np
import rrcf

# Generate data
n = 730
A = 50
center = 100
phi = 30
T = 2*np.pi/100
t = np.arange(n)
sin = A*np.sin(T*t-phi*T) + center
sin[235:255] = 80

# Set tree parameters
num_trees = 40
shingle_size = 4
tree_size = 256

# Create a forest of empty trees
forest = []
for _ in range(num_trees):
    tree = rrcf.RCTree()
    forest.append(tree)
    
# Use the "shingle" generator to create rolling window
points = rrcf.shingle(sin, size=shingle_size)

# Create a dict to store anomaly score of each point
avg_codisp = {}

# For each shingle...
for index, point in enumerate(points):
    # For each tree in the forest...
    for tree in forest:
        # If tree is above permitted size, drop the oldest point (FIFO)
        if len(tree.leaves) > tree_size:
            tree.forget_point(index - tree_size)
        # Insert the new point into the tree
        tree.insert_point(point, index=index)
        # Compute codisp on the new point and take the average among all trees
        if not index in avg_codisp:
            avg_codisp[index] = 0
        avg_codisp[index] += tree.codisp(index) / num_trees

计算结果展示

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

fig, ax1 = plt.subplots(figsize=(10, 5))

color = 'tab:red'
ax1.set_ylabel('Data', color=color, size=14)
ax1.plot(sin, color=color)
ax1.tick_params(axis='y', labelcolor=color, labelsize=12)
ax1.set_ylim(0,160)
ax2 = ax1.twinx()
color = 'tab:blue'
ax2.set_ylabel('CoDisp', color=color, size=14)
ax2.plot(pd.Series(avg_codisp).sort_index(), color=color)
ax2.tick_params(axis='y', labelcolor=color, labelsize=12)
ax2.grid('off')
ax2.set_ylim(0, 160)
plt.title('Sine wave with injected anomaly (red) and anomaly score (blue)', size=14)

14.3 总结

异常检测任重而道远，RRCF 可以作为经典机器学习算法的一个代表进行对比实验。可以说是比较先进的代表了。

论文的表述方式有点不习惯，但是大致意思应该是可以看懂的，如果还有什么疑问欢迎在下方留言，我们一起讨论一下吧。

Smileyan
2021.11/28 18:09

[1] 论文地址
[2] 源码地址