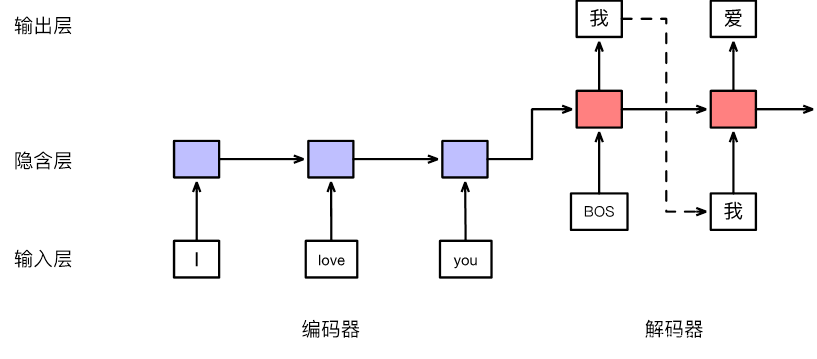
一、RNN

前馈神经网络：信息往一个方向流动。包括MLP和CNN
循环神经网络：信息循环流动，网络隐含层输出又作为自身输入，包括RNN、LSTM、GAN等。

RNN模型结构如下图所示：

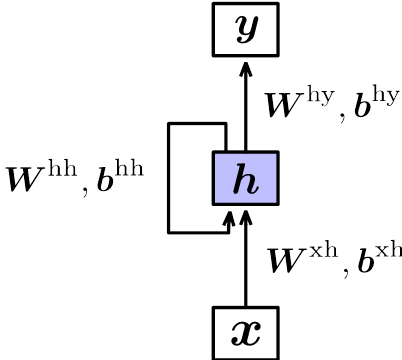
展开之后相当于堆叠多个共享隐含层参数的前馈神经网络：

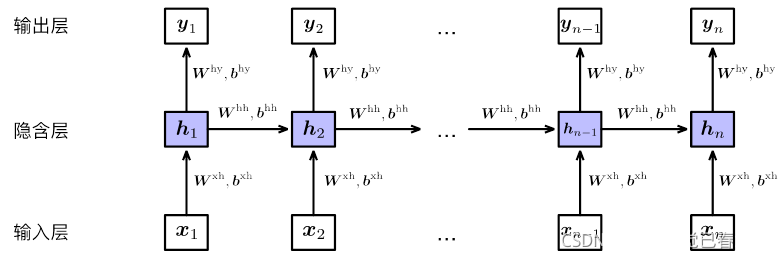
其输出为：
$${\mathbf{h}}_{\mathbf{t}}=\mathbf{t}\mathbf{a}\mathbf{n}\mathbf{h}({\mathbf{W}}^{\mathbf{x}\mathbf{h}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{b}}^{\mathbf{x}\mathbf{h}}+{\mathbf{W}}^{\mathbf{h}\mathbf{h}}{\mathbf{h}}_{\mathbf{t}-1}+{\mathbf{b}}^{\mathbf{h}\mathbf{h}})$$
$${\mathbf{y}}_{\mathbf{n}}=\mathbf{s}\mathbf{o}\mathbf{f}\mathbf{t}\mathbf{m}\mathbf{a}\mathbf{x}({\mathbf{W}}^{\mathbf{h}\mathbf{y}}{\mathbf{h}}_{\mathbf{n}}+{\mathbf{b}}^{\mathbf{h}\mathbf{y}})$$

• 即隐含层输入不但与当前时刻输入$x_t$有关，还与前一时刻隐含层$h_{t-1}$有关。每个时刻的输入经过层层递归，对最终输入产生一定影响。
• 每个时刻隐含层$h_t$包含1~t时刻全部输入信息，所以隐含层也叫记忆单元（Memory）
• 每个时刻参数共享（‘循环’的由来）
• 每个时刻也可以有相应的输出（序列标注）

二、长短时记忆网络LSTM

RNN的缺点是信息经过多个隐含层传递到输出层，会导致信息损失。更本质地，会造成网络参数难以优化。LSTM加入全局信息context，可以解决这一问题。

1. 跨层连接
LSTM首先将隐含层更新方式改为：
$${\mathbf{u}}_{\mathbf{t}}=\mathbf{t}\mathbf{a}\mathbf{n}\mathbf{h}({\mathbf{W}}^{\mathbf{x}\mathbf{h}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{b}}^{\mathbf{x}\mathbf{h}}+{\mathbf{W}}^{\mathbf{h}\mathbf{h}}{\mathbf{h}}_{\mathbf{t}-1}+{\mathbf{b}}^{\mathbf{h}\mathbf{h}})$$
$${\mathbf{h}}_{\mathbf{t}}={\mathbf{h}}_{\mathbf{t}-1}+{\mathbf{u}}_{\mathbf{t}}$$

这样可以直接将$h_k$与$h_t$相连，实现跨层连接，减小网络层数，使得网络参数更容易被优化。证明如下：
$${\mathbf{h}}_{\mathbf{t}}={\mathbf{h}}_{\mathbf{t}-1}+{\mathbf{u}}_{\mathbf{t}}={\mathbf{h}}_{\mathbf{t}-2}+{\mathbf{u}}_{\mathbf{t}-1}+{\mathbf{u}}_{\mathbf{t}}=...={\mathbf{h}}_{\mathbf{k}}+{\mathbf{u}}_{\mathbf{k}+1}+{\mathbf{u}}_{\mathbf{k}+2}+...+{\mathbf{u}}_{\mathbf{t}-1}+{\mathbf{u}}_{\mathbf{t}}$$

2. 增加遗忘门 forget gate
   上式直接将旧状态$h_{t-1}$和新状态$u_t$相加，没有考虑两种状态对$h_t$的不同贡献。故计算$h_{t-1}$和$u_t$的系数，再进行加权求和
   $${\mathbf{f}}_{\mathbf{t}}=\sigma ({\mathbf{W}}^{\mathbf{f},\mathbf{x}\mathbf{h}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{b}}^{\mathbf{f},\mathbf{x}\mathbf{h}}+{\mathbf{W}}^{\mathbf{f},\mathbf{h}\mathbf{h}}{\mathbf{h}}_{\mathbf{t}-1}+{\mathbf{b}}^{\mathbf{f},\mathbf{h}\mathbf{h}})$$
   $${\mathsf{h}}_{\mathsf{t}}={\mathsf{f}}_{\mathsf{t}}\odot {\mathsf{h}}_{\mathsf{t}-1}+(1-{\mathsf{f}}_{\mathsf{t}})\odot {\mathsf{u}}_{\mathsf{t}}$$
   其中$\sigma$表示sigmoid函数，值域为（0，1）。当$f_t$较小时，旧状态贡献也较小，甚至为0，表示遗忘不重要的信息，所以称为遗忘门。
3. 增加输入门 Input gate
   上一步问题是旧状态$h_{t-1}$和新状态$u_t$权重互斥。但是二者可能都很大或者很小。所以需要用独立的系数来调整。即：
   $${\mathbf{i}}_{\mathbf{t}}=\sigma ({\mathbf{W}}^{\mathbf{i},\mathbf{x}\mathbf{h}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{b}}^{\mathbf{i},\mathbf{x}\mathbf{h}}+{\mathbf{W}}^{\mathbf{i},\mathbf{h}\mathbf{h}}{\mathbf{h}}_{\mathbf{t}-1}+{\mathbf{b}}^{\mathbf{i},\mathbf{h}\mathbf{h}})$$
   $${\mathsf{h}}_{\mathsf{t}}={\mathsf{f}}_{\mathsf{t}}\odot {\mathsf{h}}_{\mathsf{t}-1}+{\mathsf{i}}_{\mathsf{t}}\odot {\mathsf{u}}_{\mathsf{t}}$$
   $i_t$用于控制输入状态$u_t$对当前状态的贡献，所以称为输入门
4. 增加输出门output gate
   $${\mathbf{o}}_{\mathbf{t}}=\sigma ({\mathbf{W}}^{\mathbf{o},\mathbf{x}\mathbf{h}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{b}}^{\mathbf{o},\mathbf{x}\mathbf{h}}+{\mathbf{W}}^{\mathbf{o},\mathbf{h}\mathbf{h}}{\mathbf{h}}_{\mathbf{t}-1}+{\mathbf{b}}^{\mathbf{o},\mathbf{h}\mathbf{h}})$$
5. 综合计算
   $${\mathbf{u}}_{\mathbf{t}}=\mathbf{t}\mathbf{a}\mathbf{n}\mathbf{h}({\mathbf{W}}^{\mathbf{x}\mathbf{h}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{b}}^{\mathbf{x}\mathbf{h}}+{\mathbf{W}}^{\mathbf{h}\mathbf{h}}{\mathbf{h}}_{\mathbf{t}-1}+{\mathbf{b}}^{\mathbf{h}\mathbf{h}})$$
   $${\mathbf{f}}_{\mathbf{t}}=\sigma ({\mathbf{W}}^{\mathbf{f},\mathbf{x}\mathbf{h}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{b}}^{\mathbf{f},\mathbf{x}\mathbf{h}}+{\mathbf{W}}^{\mathbf{f},\mathbf{h}\mathbf{h}}{\mathbf{h}}_{\mathbf{t}-1}+{\mathbf{b}}^{\mathbf{f},\mathbf{h}\mathbf{h}})$$
   $${\mathbf{i}}_{\mathbf{t}}=\sigma ({\mathbf{W}}^{\mathbf{i},\mathbf{x}\mathbf{h}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{b}}^{\mathbf{i},\mathbf{x}\mathbf{h}}+{\mathbf{W}}^{\mathbf{i},\mathbf{h}\mathbf{h}}{\mathbf{h}}_{\mathbf{t}-1}+{\mathbf{b}}^{\mathbf{i},\mathbf{h}\mathbf{h}})$$
   $${\mathbf{c}}_{\mathbf{t}}={\mathbf{f}}_{\mathbf{t}}\odot {\mathbf{c}}_{\mathbf{t}-1}+{\mathbf{i}}_{\mathbf{t}}\odot {\mathbf{u}}_{\mathbf{t}}$$
   $${\mathbf{h}}_{\mathbf{t}}={\mathbf{o}}_{\mathbf{t}}\odot \mathbf{t}\mathbf{a}\mathbf{n}\mathbf{h}({\mathbf{c}}_{\mathbf{t}})$$

• 遗忘门：$f_t$，是$c_{t-1}$的系数，可以过滤上一时刻的记忆信息
• 输入门：$i_t$，是$u_t$的系数，可以过滤当前时刻的输入信息
• 输出门：$o_t$，是$tanh(c_t)$的系数，控制记忆信息
• 记忆细胞：$c_t$，记录了截止当前时刻的重要信息。

可以看出RNN的输入层隐含层和输出层三层都是共享参数，到了LSTM都变成参数不共享了。

2.2 双向循环神经网络Bi-LSTM

• 解决循环神经网络信息单向流动的问题。（比如一个词的词性与前面的词有关，也与自身及后面的词有关）
• 将同一个输入序列分别接入前向和后向两个循环神经网络中，再将两个循环神经网络的隐含层结果拼接在一起，共同接入输出层进行预测。其结构如下：
  
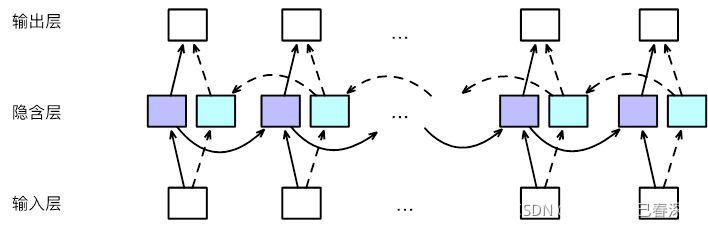
  此外还可以堆叠多个双向循环神经网络。
  LSTM比起RNN多了最后时刻的记忆细胞，即：

bilstm=nn.LSTM(
        input_size=1024, 
        hidden_size=512, 
        batch_first=True,
        num_layers=2,#堆叠层数
        dropout=0.5,  
        bidirectional=True#双向循环)

hidden, hn = self.rnn(inputs)
#hidden是各时刻的隐含层，hn为最后时刻隐含层
hidden, (hn, cn) = self.lstm(inputs)
#hidden是各时刻的隐含层，hn, cn为最后时刻隐含层和记忆细胞

三、序列到序列模型