优化算法进行神经网络的参数寻优，解放深度调参

最近先立个flag，用python把目前的主流的、新的智能算法与神经网络的参数优化相结合，进行自动参数寻优。寻优参数，不用限制形式，待寻优参数可以使网络层数、激活函数、优化器、初始学习率、网络块的结构、卷积的方式、核大小、步幅、初始化方式、神经元数目、神经元类型等但凡能想得到的“参数”

目前，已经使用了GA算法、PSO算法和SSA算法优化CNN网络进行涡扇发动机数据集的剩余使用寿命预测：

def main():
    """进化一个网络."""
    generations = 50  # 种群进化代数.
    population = 10  # 种群数量.
    dataset = 'C-MAPSS'
    #random.randint()方法里面的取值区间是前闭后闭区间，而np.random.randint()方法的取值区间是前闭后开区间
    #[a for a in np.arange(1,129,2)]
    nn_param_choices = {
        'activation':['relu', 'elu', 'selu', 'LeakyReLU'],
        'optimizer':['Adam', 'RMSprop', 'Adagrad', 'Adadelta', 'Adamax','Nadam'],
        'layer_1': [4,8,16,24,32,36,48,64,80,100,128],
        'layer_2': [0,4,8,16,24,32,36,48,64,80,100,128],
        'layer_3': [0,4,8,16,24,32,36,48,64,80,100,128],
        'layer_4': [0,4,8,16,24,32,36,48,64,80,100,128],
        'kernel_size':[2,3],
        'Dropout': [0,0.10,0.15,0.20,0.25,0.30],
        'alpha':[0.05,0.1,0.15,0.2,0.25,0.3],
        'batch_size':[32,64,128],
        'decay':[1e-6,5e-6,1e-5,5e-5,1e-4,5e-4],
        'learning_rate':[0.0001,0.0005,0.001,0.005,0.01,0.05,0.1,0.5,1.0]
    }
    #'learning_rate':[0.0001,0.0005,0.0008,0.001,0.005,0.008,0.01,0.05,0.08,0.1]
    logging.info("***当前进化代数 %d 当前代数种群数量 %d***" %
                 (generations, population))

    generate(generations, population, nn_param_choices, dataset)
if __name__ == '__main__':
    main()

1.已经实现的Genetic Algorithm优化Neural Network

GA参数搜索的可视化过程：

2.已经实现的PSO优化Neural Network

参数搜索和GA通用，单独修改了算法代码。PSO参数搜索可视化过程：

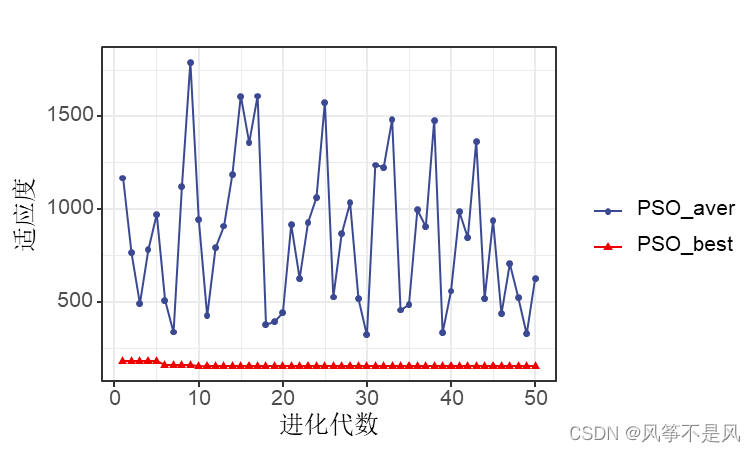
3.已实现的SSA¹优化Neural Network

参数搜索和GA通用，单独修改了算法代码。SSA参数搜索可视化过程：

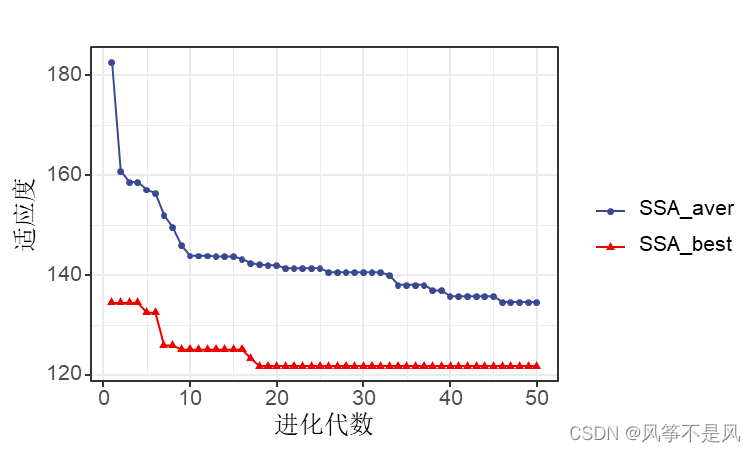
三种方法的可视化搜索过程对比

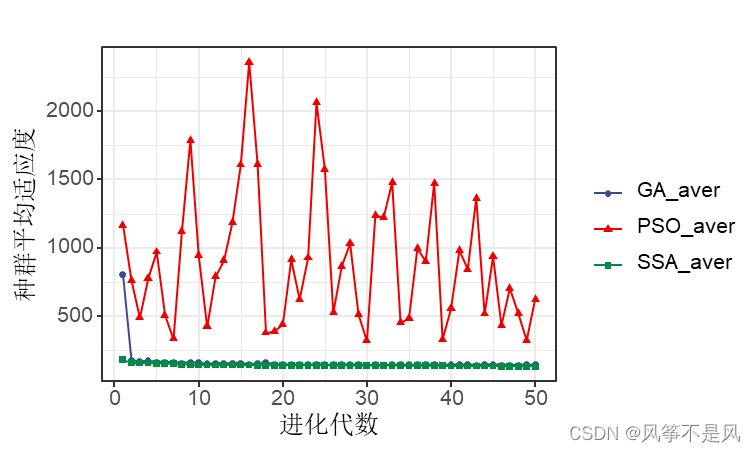
1）三种算法的种群平均适应度的比较

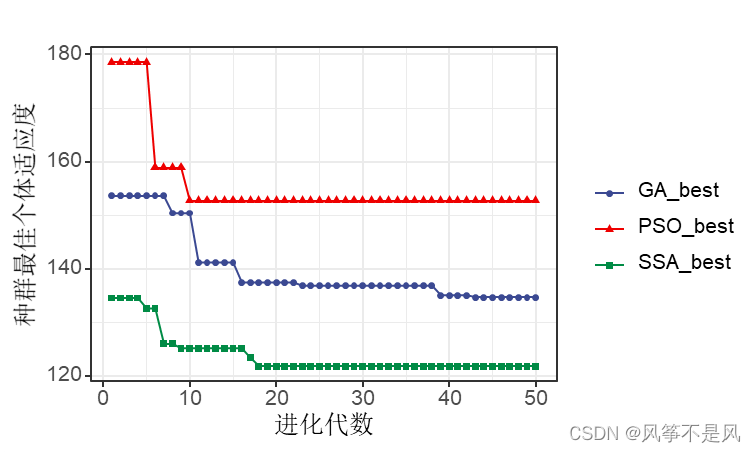
2）种群最佳个体适应度

三种优化算法性能总结

GA、PSO和SSA三种优化算法的性能总结：

项目	收敛速度	收敛值
GA	最慢	较小
PSO	最快	最大
SSA	较快	最小

总结

优化算法搜索出来的神经网络模型效果确实是有一定的提升，但是未必能保证后续每一次运行的结果就能达到优化时那么好的效果。

目前来将任何新出的智能优化算法都可以做神经网络的参数搜索，并且都比较容易应用

可以使用UML图表进行渲染。 Mermaid. 例如下面产生的一个序列图：

---

1. Xue, J., & Shen, B. (2020). A novel swarm intelligence optimization approach: sparrow search algorithm. Systems Science & Control Engineering, 8(1), 22-34. ↩︎