智能优化算法：水基湍流优化算法

摘要：水基湍流优化算法（Turbulent Flow of Water-based Optimization，TFWO）是于2020年，提出的一种新型智能优化算法。灵感来自于一个自然搜索现象，即在湍流中产生的漩涡，实现全局搜索。该算法消除了控制参数选择问题，提高了收敛能力，并且具有固定的结构。与其他优化算法相比，该算法具有更好的竞争性和鲁棒性。

1.算法原理

1.1 漩涡模型

漩涡模型如图1所示：对于匀速圆周运动的物体，圆的半径($r$)等于物体质量($m$)与速度平方乘以向心力($Fc$)的乘积。此外，质量和离心力，以及相邻漩涡和物体之间的相互作用，导致了这种牵引和吸引的阻力和偏差。首先，我们把算法的总体划分为 $N_{Wh}$ ,每个组的最佳成员代表了漩涡的牵引强度。将各组最佳成员设置在相应漩涡的中心，形成孔洞。以及漩涡中心的牵引力。团队中最好的成员试图统一粒子的位置和他们的漩涡中心(团队中最好的成员的位置) ，并把他们拉进洞里。围绕在物体周围的漩涡在物体的相反方向向漩涡的洞(群体中最好的成员)作出一个特定的距离，以某种方式减少了牵引力和向心力，并使它远离漩涡的中心。离心力可能会对向心力造成不良影响及/或破坏或改变物件。而且，较大和较强的漩涡会根据方向和距离对较小和较弱的漩涡进行拉力或推力，相互影响各自的位置，改变其他漩涡的位置。在下文中，根据上述段落介绍了该算法的实现和性能步骤，并对其进行了建模:

图1.漩涡模型

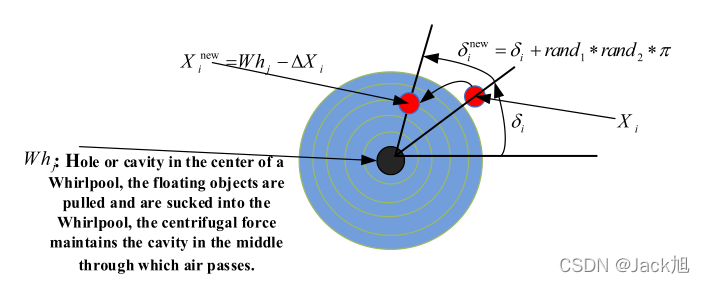
1.2漩涡的形成

首先将算法的初始种群$X^0$平均分配给$N_p$组漩涡集，然后将每个漩涡集中最强的成员视为拉动对象的漩涡.。

1.3 漩涡对其内在和其他漩涡的影响

每个漩涡($Wh$)充当一个吸水井或者吸水洞，并且倾向于通过在它们上面施加一个向心力来统一其中心位置($X$)中物体的位置，然后将它们投入到它的井中。因此，漩涡在$W{h}_j$上的局部位置，以统一物体($X_i$)和它自己的位置的方式作用，即$X_i=W{h}_j$。尽管如此，其他漩涡会根据它们之间的距离($Wh-W{h}_j)$和目标值产生一些偏差($\Delta X$)。因此，该物体的新位置等于 $X_i^{New}=W{h}_j-\Delta X_i$，其中漩涡对其物体的影响如图1所示。

如图1所示，物体($x$)以它们特殊的角度($\delta$)绕着漩涡的中心移动并接近它。因此，这个角度在每一个时刻(迭代的算法)是变化的:
$${\delta }_i^{new}={\delta }_i+ran{d}_1\ast ran{d}_2\ast \pi \text{\hspace{1em}(1)}$$
根据公式（2）计算最远和最近的漩涡，即与所有物体的最大和最小距离的漩涡。利用式（3）计算$\Delta X_i$。利用式（4）更新位置
$${\Delta }_t=f(W{h}_t)\ast |W{h}_t-sum(X_i){|}^{0.5}\text{\hspace{1em}(2)}$$

$$\begin{gathered} \Delta X_i=(cos({\delta }_i^{new})\ast rand(1,D)\ast (W{h}_f-X_i)-sin({\delta }_i^{new})\ast rand(1,D)\ast (W{h}_w-X_i)) \\ \ast (1+|cos({\delta }_i^{new})-sin({\delta }_i^{new})|)\text{\hspace{1em}(3)} \end{gathered}$$

$$X_i^{new}=W{h}_j-\Delta X_i\text{\hspace{1em}(4)}$$

其中$W{h}_f$和$W{h}_w$分别为角度$\Delta t$最小值和最大值的漩涡，$\delta i$为对$i$个对象的角度。

1.4 离心力

虽然向心力把移动的物体拉向它们的漩涡，离心力却把它们从相应的中心带走。根据牛顿第一运动定律，静止的物体保持静止，运动的物体保持相同的速度和方向，除非受到不平衡力的作用。离心力(或者)有时克服了向心力或者旋涡的牵引力，将物体随机转移到一个新的位置。在这里，我们模拟了离心力$F{E}_i$。式(5)在决策变量的一个维度中随机发生。为了达到这个目的，首先离心力是根据物体和漩涡之间的角度来计算的见式（5），如果这个力大于一个随机值(在范围内均匀分布[0,1])时，按式（6）计算离心力。
$$F{E}_i=((cos({\delta }_i^{new}){)}^2\ast (sin({\delta }_i^{new}){)}^2)\text{\hspace{1em}(5)}$$

$$x_{i,p}=x_p^{min}+rand\ast (x_p^{max}-x_p^{min})\text{\hspace{1em}(6)}$$

1.5 漩涡之间的相互作用

类似于漩涡对周围物体的影响，它们也相互作用和移动。这种效果被模拟为物体上的漩涡效果，每个漩涡倾向于拉动其他漩涡，在它们上面施加向心力，并把它们投入它们的井中(即统一考虑漩涡的位置和它自己的位置)。为了模拟这种效应，首先根据最近的漩涡的目标函数和当量的最小值计算出最近的漩涡见式（7）和式（8），式（9）用于更新漩涡的位置。
$$\Delta t=f(W{h}_t)\ast |W{h}_t-sum(W{h}_j)|\text{\hspace{1em}(7)}$$

$$\Delta W{h}_j=rand(1,D)\ast |cos({\delta }_j^{new})+sin({\delta }_j^{new})|\ast (W{h}_f-W{h}_j)\text{\hspace{1em}(8)}$$

$$W{h}_j^{new}=W{h}_f-\Delta W{h}_j\text{\hspace{1em}(9)}$$

其中：${\delta }_j$为第$j$个漩涡洞的角度。

算法流程：

步骤1：设置算法参数及初始化漩涡种群。

步骤2：评估适应度值确定初始最优位置。

步骤3：按照式（1）-（9）更新漩涡的位置。

步骤4：重新评估漩涡的位置及最优漩涡值.

步骤5：判断是否满足最大迭代次数，若满足，则输出最优位置和全局最优解，否则，返回步骤3重新迭代计算。

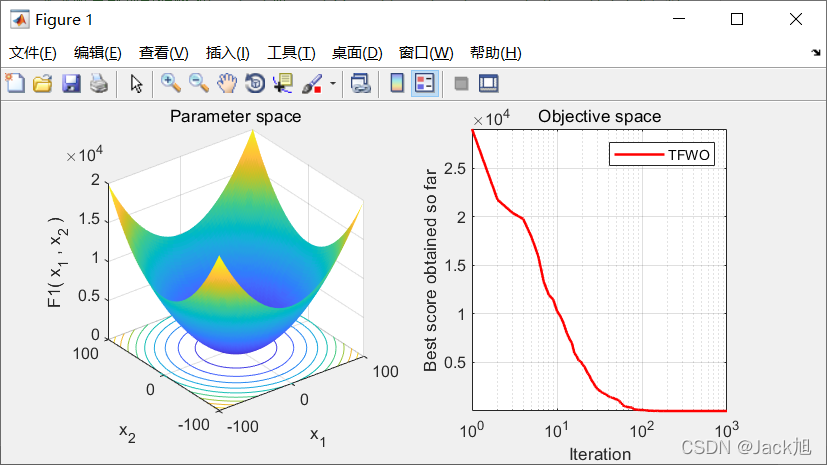
2.算法结果

3.参考文献

[1] Mojtaba Ghasemi et al., A novel and effective optimization algorithm for global optimization and its engineering applications: Turbulent Flow of Water-based Optimization (TFWO). Engineering Applications of Artificial Intelligence.

4.Matlab