4.6.1 two pointers（双指针）

以一个例子引入：给定一个递增的正整数序列和一个正整数M，求序列中的两个不同位置的数a和数b，使得他们的和恰好为M，输出所有满足条件的方案。例如给定序列{1,2,3,4,5,6}和正整数M=8，则存在2+6=8 , 3+5=8成立。
最直接的双重遍历：

    for( int i = 0 ; i < n ; i++ ){
        for( int j = i+1 ; j < n ; j++ ){
            if( a[i] + a[j] == M ){
                cout << i << " " << j << endl ;
            }
        }
    }

显然，这种做法的时间复杂度为O(n²)，对n在10^5的规模时是不可接受的。
事实上，本题采用双指针利用有序序列的枚举特性来有效降低时间复杂度。过程如下：
令下标i的初值为0，下标j的初值为n-1,即令i、j分别指向序列的第一个元素与最后一个元素，接下来根据a[i]+a[j]与M的大小来进行下面三种选择：使i不断向右移动、使j不断向左移动、如果a[i]+a[j]==M,同时让i向右移动，j向左移动。直到i>=j 。
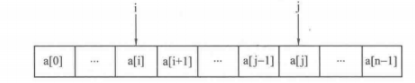
在这里插入图片描述

如果满足a[i]+a[j] == M ,说明找到了其中一个方案。由于序列递增，a[i+1]+a[j]>M肯定成立，a[i]+a[j-1]<M也成立，但是a[i+1]+a[j-1]与M的关系不能推测，所以令i=i+1 , j = j-1(即令i向右移动，j向左移动)。
如果满足a[i]+a[j] > M , 由于序列递增，a[i+1]+a[j]>M肯定成立，但是不能确定a[i]+a[j-1]与M的关系，所以令j=j-1（即j向左移动）。
如果满足a[i]+a[j]<M,同理，令a=a+1（即令i向右移动）。
反复执行以上步骤，直到i>=j 。

    while( i < j ){
        if( a[i] + a[j] == M ){
            cout << i << " " << j << endl ;
            i ++ ;
            j -- ;
        }
        else if( a[i] + a[j] > M ){
            j -- ;
        }
        else{
            i ++ ;
        }
    }

时间复杂度为O(n)。

序列归并问题

假设有两个递增的序列A与B，要求将它们合并为一个递增序列C。
同样的，可以设置两个下标i和j，初值均为0，分别表示序列A的第一个元素和序列B的第一个元素，然后根据A[i]与B[j]的大小决定哪一个放入序列C。

如果A[i] <= B[j]，则把A[i]放入C的末尾，并将i++。
如果A[i] > B[j] ，则把B[j]放入C的末尾，并将j++。
直到i,j中的一个到达序列末尾，然后将另一个序列的所有元素一次放入C。

    /*
        vector<int> a 为升序序列1
        vector<int> b 为升序序列2
        int L1 , int R1 为序列1的取值区间[L1,R1]
        int R1 , int R2 为序列2的取值区间[L2,R2]
    */
    vector<int> Merge(vector<int> a , vector<int> b , int L1 , int R1 , int R1 , int R2 ){
        int i = L1 ;
        int j = L2 ;
        vector<int> ans ; //暂存合并后的序列
        //只要其中一个序列还没有遍历结束
        while( i <= R1 && j <= R2 ){
            if( a[i] <= b[j] ){
                ans.push_back(a[i++]) ;
            }
            else{
                ans.push_back(b[j++]) ;
            }
        }
        //如果序列a还没完，将剩余的加到ans上
        while( i <= R1 ){
             ans.push_back(a[i++]) ;
        }
        //如果序列b还没完，将剩余的加到ans上
        while( j <= R2 ){
             ans.push_back(b[j++]) ;
        }
        return ans ; //返回合并后的序列
    }

4.6.2 归并排序

2路归并排序，时间复杂度为O(nlogn)。
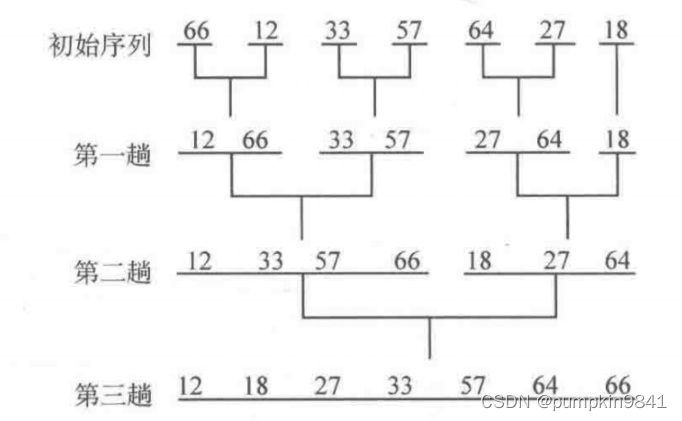
在这里插入图片描述

2-路归并排序的核心在于如何将两个有序序列合并为一个有序序列。

1.递归实现

反复将当前区间[left,right]分为两半，对两个子区间[left , mid]、[mid+1,right]分别递归进行归并排序，然后将两个已经有序的子区间合并为有序序列。

const int maxn = 100 ;
//将数组A的[L1,R1]与[L2,R2]合并为有序区间(此处L2即为R1+1)
void merge( int A[] , int L1 , int R1 , int L2 , int R2 ){
    int i = L1 ;
    int j = L2 ;
    int temp[maxn]; //暂存合并后的数组
    int index = 0 ; //index为temp下标
    while( i <= R1 && j <= R2 ){
        if( A[i] <= A[j] ){
            temp[index++] = A[i++] ;
        }
        else{
            temp[index++] = A[j++] ;
        }
    }

    //将[L1,R1]剩余元素加入序列temp
    while( i <= R1 ){
        temp[index++] = A[i++] ;
    }
    //将[L2,R2]剩余元素加入序列temp
    while( j <= R2 ){
        temp[index++] = A[j++] ;
    }

    for( int i = 0 ; i < index ; i++ ){
        A[L1+i] = temp[i] ;     //将合并后的序列赋值给数组A
    }
}

//将array数组当前区间[left , right]进行归并排序
void mergeSort( int A[] , int left , int right ){
    if( left < right ){
        int mid = (left + right) / 2 ;  //取区间终点
        mergeSort(A , left , mid) ;   //递归，将左子区间归并排序
        mergeSort(A , mid+1 , right) ;  //递归，将右子区间归并排序
        merge(A , left , mid , mid+1 , right) ;     //将左子区间和右子区间合并
    }
}

非递归实现

当然，如果题目中只要求给出归并排序每一趟结束时的序列，那么完全可以使用sort函数代替merge(只要时间限制允许)。

void mergeSort( int A[] ){
    int n = A.size() - 1 ;
    //step为组内元素个数，step/2为左子区间元素个数，注意等号可以不取
    for( int step = 1 ; step /2 <= n ; step *= 2 ){
        //每step个元素一组，组内[i , min(i+step , n+1)]进行排序
        for( int i = 1 ; i <= n ; i+=step ){
            sort( A+i , A+min( i+step , n+1 ) )
        }
        //此处可以输出归并排序的某一趟序列
    }
    
}

4.6.3 快速排序

快速排序时排序算法中平均时间复杂度为O(nlogn)的一种算法。
其思想是，对一个序列A[1]、A[2]、A[3]……A[n] ，每一趟快速排序确定序列中一个元素A[x]的位置，使得A[x]左边的元素全部不超过A[x]，使得A[x]右侧的元素全部大于A[x]。例如
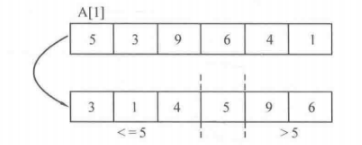
在这里插入图片描述

经过一趟排序后，确定了A[1]=5的位置。
利用tow pointers思想做法：

将A[1]存至临时变量temp，并令下标left、right分别只想序列的第一个元素与最后一个元素(如令left = 0 , right = n-1)。
只要right指向的元素A[right] > temp ，就right不断向左移；当某个时候A[right]<= temp时，令A[left] = A[right]
只要left指向的元素A[left] <= temp ，就将left不断向右移；当某个时候A[left] > temp时，令A[right] = A[left]
重复2、3，直到left与right相遇，把temp放到相遇的位置。

可以很容易写出这部分代码，其中用以划分区间的元素A[left]被称为主元。

//对区间[left,right]进行划分
int Partition( int A[] , int left , int right ){
    int temp = A[left] ;   //将A[left]存至临时变量temp
    while( left < right ){
        while(  left < right && A[right] > temp ){
            right -- ;          //反复左移
        }   
        A[left] = A[right] ;
        while( left < right && A[left] <= temp ){
            left ++ ;           //反复右移
        }
        A[right] = A[left] ;
        
    }
    A[left] = temp ;  //把temp放到left与right相遇的位置
    return left ;    //返回相遇的下标
}

//递归实现快速排序
void quickSort( int A[] , int left , int right ){
    if( left < right ){
        int pos = Partition( A , left , right ) ;
        quickSort(A , left , pos - 1 ) ;    //对左子区间递归进行快排
        quickSort(A , pos + 1 , right ) ;   //对右子区间递归进行快排
    }
}

快速排序算法在序列中元素的排列比较随机时效率最高，但是当序列中元素接近有序时，回达到最坏时间复杂度O(n²)。产生这种情况的主要原因在于主元没有把当前区间划分为两个长度接近的区间。
解决办法是随机选择主元：

int main(){
    //取随机数
    srand( (unsigned)time(NULL) );
    for( int i = 0 ; i < 10 ; i++ ){
        cout << rand()%5+3 <<endl ; //[3,7]
    }

    return 0 ;
}