写在前面
实际上,之前已经更新过一篇关于平衡树的笔记了;—>笔记链接;
学习数据结构笔记(12) — [平衡二叉搜索树(AVLTREE)]之前的实现方式需要计算出当前节点的父节点的索引;…左旋右旋实现方式步骤比较明确;
不足之处是仅实现了添加节点时维持二分树的平衡;
本次的平衡树具体操作方式和之前的那种略有不同;所以记录一下吧…
这里的基础会以之前的二分搜索树实现作为基础,在基础上进行改动;笔记链接—>
数据结构 (五) — [二分搜索树 (Java)]
这里首先会在节点内定义属性height表示高度;
然后在树中定义基础方法来获取树的高度;
基础方法获取树的平衡因子:—>左右子树的高度差;
定义了方法 判断当前树是否为二分搜索树(判断中序遍历的结果是否为由小到大排序);
当前树是否为平衡树(平衡因子是否超过1);
以及添加/删除节点时左旋右旋操作维持二分树的平衡;
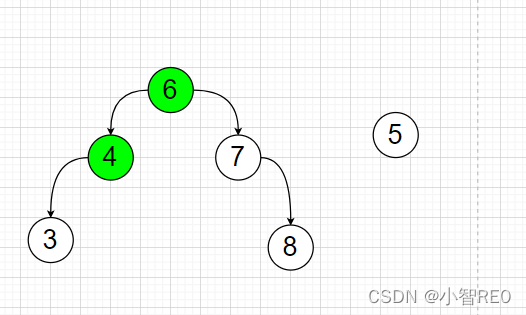
如图,这不是平衡树
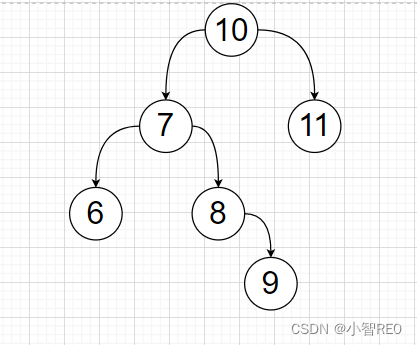
文章目录
- 右旋转
- 左旋转
- 双旋转
- 具体代码
- 删除方法优化
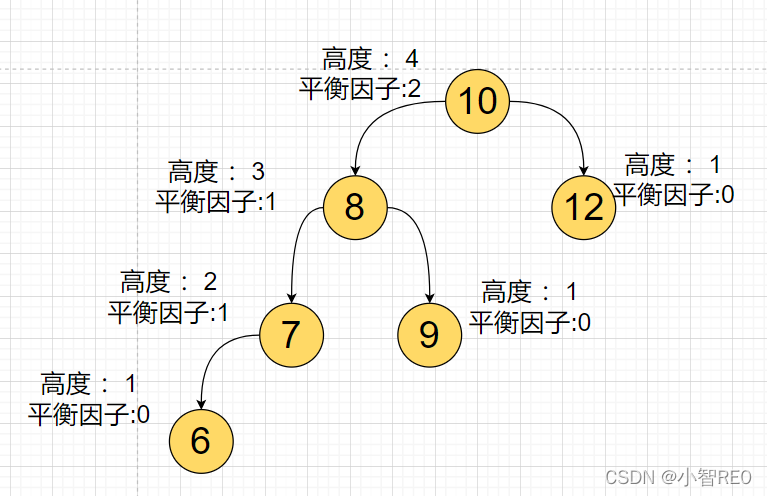
右旋转
这棵树左子树偏高;要进行右旋转
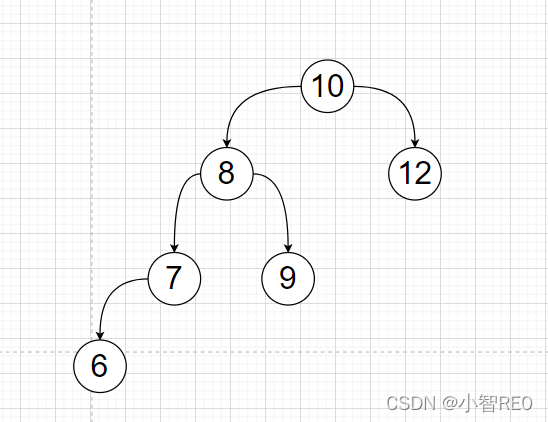
那么,仅需两步;
首先将取出节点8的右子节点9;将节点10作为节点8的右子节点
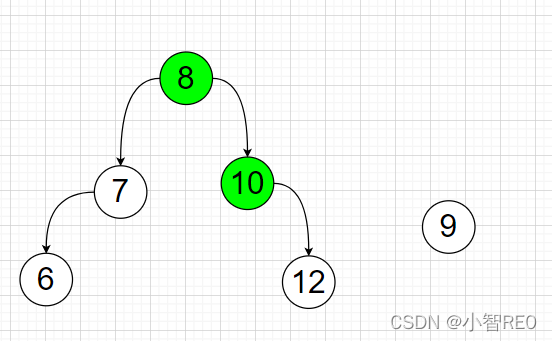
然后让
节点9作为节点10的左子节点
左旋转
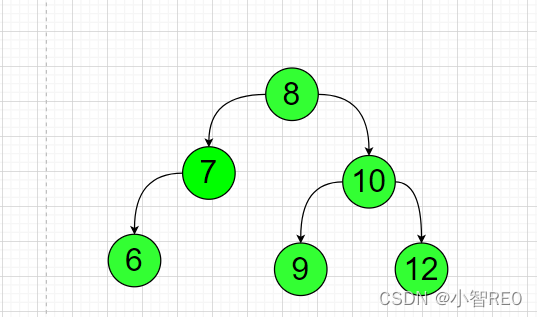
这棵树右子树偏高,需要左旋转
只需两步;
首先将节点6的左子节点5取出,记录;
将节点4作为节点6的左子节点
然后将节点5作为节点4的右子节点
双旋转
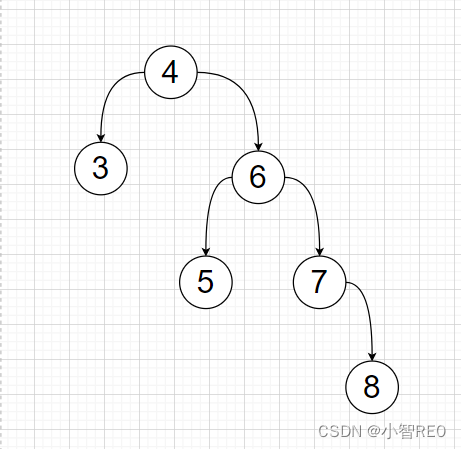
有特殊情况的,就得出动双旋转了;
像下面这种就是需要先进行左旋转处理;然后进行右旋转处理;
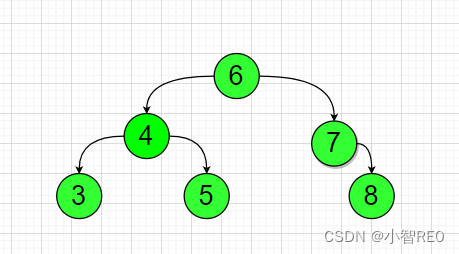
先对节点7进行左旋转处理
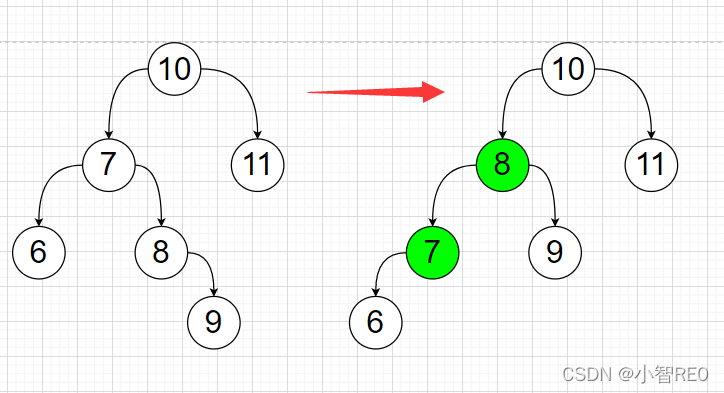
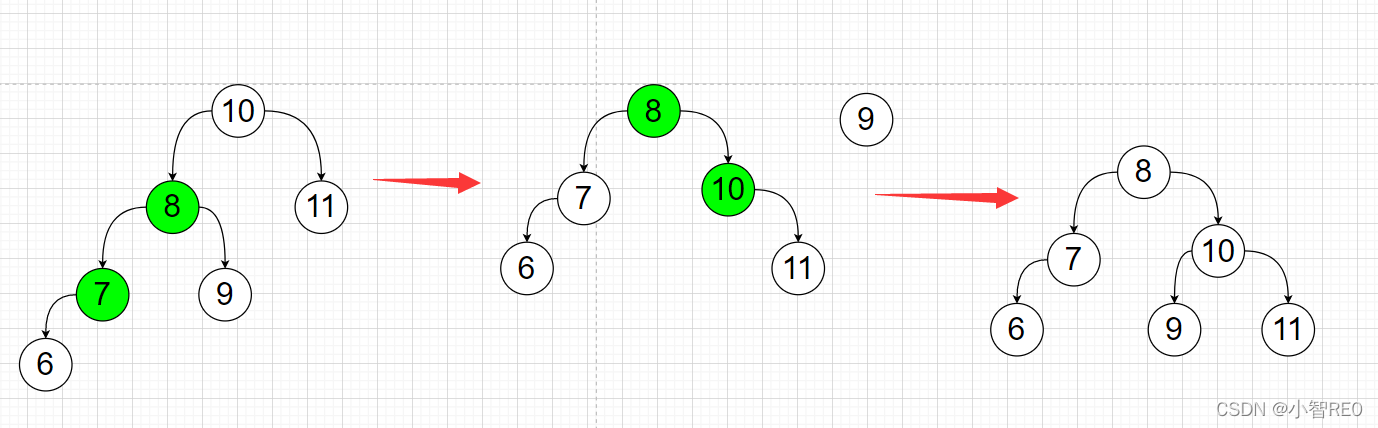
然后对节点10进行右旋转处理
具体代码
package com.company.e_avltree;
import java.util.*;
/**
* @author 小智RE0
* @Date: 2021/12/10/
*/
//由于二分搜索树,需要对元素的大小进行比较;
public class AVLStartTree<T extends Comparable<T>> {
//定义内部类结点;
class Node {
T val;
//左子树,右子树;
Node leftNode;
Node rightNode;
//树的高度;
int height;
public Node(T val) {
//初始化时,树的高度为1;
this.height = 1;
this.val = val;
this.leftNode = null;
this.rightNode = null;
}
}
//定义树的根结点;
private Node root;
//定义树结点的个数;
private int size;
public AVLStartTree() {
this.root = null;
this.size = 0;
}
//判空;
public boolean isEmpty() {
return this.root == null;
}
/**
* 获取以指定结点为树的高度
*
* @param node 节点
*/
public int getHeight(Node node) {
if (node == null) {
return 0;
} else {
return node.height;
}
}
/**
* 获取到以指定结点出发,树的高度因子;左右子树的高度差;
*/
public int getHeightFactor(Node node) {
if (node == null) {
return 0;
}
//这里没有取绝对值,可能会出现高度因子为负数的情况
return getHeight(node.leftNode) - getHeight(node.rightNode);
}
/**
* 判断是否为二分搜索树;
*/
public boolean isBSTTree() {
return isBSTTree(root);
}
/**
* 判断是否为二分搜索树
*/
private boolean isBSTTree(Node node) {
List<T> values = new ArrayList<>();
//调用递归方法;将值存到values里面;
inordertraversal(node, values);
//对遍历的值进行遍历,若为二分树,实际上会由小到大排序,若不符合,直接结束;
//注意;由于是让当前节点和后一个结点进行比较,所以循环的次数实际上会少一次;
for (int i = 0; i < values.size() - 1; i++) {
//若出现前面的比后面大,直接返回;
if (values.get(i).compareTo(values.get(i + 1)) > 0) {
return false;
}
}
return true;
}
/**
* 中序遍历,将遍历值存入集合
*
* @param node 节点
* @param values 遍历的值
*/
private void inordertraversal(Node node, List<T> values) {
//递归终止条件;
if (node == null) {
return;
}
//左中右;
inordertraversal(node.leftNode, values);
values.add(node.val);
inordertraversal(node.rightNode, values);
}
/**
* 判断是否为平衡树;
*/
public boolean isAVLTree() {
return isAVLTree(root);
}
/**
* 判断是否为平衡树
*
* @param node 节点
*/
private boolean isAVLTree(Node node) {
//递归终止的条件;
if (node == null) {
return true;
}
//判断当前节点的平衡因子;
if (Math.abs(getHeightFactor(node)) > 1) {
return false;
}
//递归计算左右子树的高度因子;
return isAVLTree(node.leftNode) && isAVLTree(node.rightNode);
}
/**
* 左旋转处理
*
* @param curNode 当前节点
*/
public Node RotateLeft(Node curNode) {
//取得当前节点的右子节点;
Node rNode = curNode.rightNode;
//将右子节点的左子节点取出,标记;
Node rLNode = rNode.leftNode;
//将当前节点作为它右子节点的左子节点;
rNode.leftNode = curNode;
//将当前节点的右子节点的 左子节点 挂接到当前节点的右子节点下;
curNode.rightNode = rLNode;
//更改树的高度;
curNode.height = Math.max(getHeight(curNode.leftNode), getHeight(curNode.rightNode)) + 1;
rNode.height = Math.max(getHeight(rNode.leftNode), getHeight(rNode.rightNode)) + 1;
return rNode;
}
/***
* 右旋转处理
* @param curNode 当前节点
*/
public Node RotateRight(Node curNode) {
//取得当前节点的左子节点;
Node lNode = curNode.leftNode;
//将左子节点的右子节点取出,标记;
Node lRNode = lNode.rightNode;
//将当前节点作为它左子节点的右子节点;
lNode.rightNode = curNode;
//将当前节点的左子节点 的 右子节点挂接到到当前节点的左子节点下;
curNode.leftNode = lRNode;
//更改树的高度;
curNode.height = Math.max(getHeight(curNode.leftNode), getHeight(curNode.rightNode)) + 1;
lNode.height = Math.max(getHeight(lNode.leftNode), getHeight(lNode.rightNode)) + 1;
return lNode;
}
/**
* 添加元素
*
* @param ele 指定的元素
*/
public void add(T ele) {
//判断节点是否存在;
if (contains(ele) != null) {
return;
}
//每次将创建的根节点返回;
root = add(root, ele);
this.size += 1;
}
//递归添加元素的底层;
private Node add(Node node, T ele) {
//不存在就创建;
if (node == null) {
return new Node(ele);
}
//添加的元素和之前的根结点进行比较;
if (ele.compareTo(node.val) > 0) {
node.rightNode = add(node.rightNode, ele);
} else {
node.leftNode = add(node.leftNode, ele);
}
//添加之后;需要更新当前树的高度,----->计算左右子树的高度+1 作为当前树的高度;
node.height = Math.max(getHeight(node.leftNode), getHeight(node.rightNode)) + 1;
//左旋转,右旋转,以及左右旋转情况判断;
Node resNode = null;
//维持平衡;
//极度偏左;
if (getHeightFactor(node) > 1 && getHeightFactor(node.leftNode) >= 0) {
//直接右旋;
resNode = RotateRight(node);
}
//极度偏右;
else if (getHeightFactor(node) < -1 && getHeightFactor(node.rightNode) <= 0) {
//直接左旋;
resNode = RotateLeft(node);
}
//左树先偏高,后面右子树偏高;
else if (getHeightFactor(node) > 1 && getHeightFactor(node.leftNode) < 0) {
//先左旋后右旋;
node.leftNode = RotateLeft(node.leftNode);
resNode = RotateRight(node);
}
//右树先偏高,后面左子树偏高;
else if (getHeightFactor(node) < -1 && getHeightFactor(node.rightNode) > 0) {
//先右旋再左旋;
node.rightNode = RotateRight(node.rightNode);
resNode = RotateLeft(node);
} else {
//若平衡,就直接用node节点的值;
resNode = node;
}
return resNode;
}
/**
* 删除指定数值;
* @param val 指定数值;
*/
public T removeAssignVal(T val) {
if (root == null) {
System.out.println("空树不用删除");
return null;
}
//先去找是否存在; 要去新建方法;
Node node = findAssignNode(root, val);
//是否找到;
if (node != null) {
//删除后的剩余结点挂到根结点之后;
root = removeAssignVal(root, val);
//元素个数减少;
this.size -= 1;
return node.val;
}
return null;
}
/**
* 删除指定结点的底层实现;在根结点为node的二分树中删除指定结点;
*
* @param node 指定根结点出发
* @param val 指定值
*/
private Node removeAssignVal(Node node, T val) {
//找到结点时;
if (node.val.compareTo(val) == 0) {
//第一种情况==> 该删除结点的左树为空;
if (node.leftNode == null) {
//删除当前的结点后;把原来后面的右子树挂到删了结点的位置;
Node RNode = node.rightNode;
node.rightNode = null;
return RNode;
}
//第二种情况,右树为空;
else if (node.rightNode == null) {
//删除当前的结点后;把原来后面的左子树挂到删了结点的位置;
Node LNode = node.leftNode;
node.leftNode = null;
return LNode;
} else {
//情况三; 左树 右树 都不为空时,可以选择找前驱结点(左子树那块区域的最大值) 或 后继结点(右子树那块区域的最小值)代替删除结点;
//这里选择找后继节点;
Node minR = findMinNodeRecurve(node.rightNode);
Node minRNode = removeMinNode(node.rightNode);
//后继节点放到删除的结点位置;
minR.leftNode = node.leftNode;
minR.rightNode = minRNode;
node.leftNode = null;
node.rightNode = null;
return minR;
}
}
//递归;
//找结点时,若当前的根结点比指定的值还大,就去左边找; 否则去右边找;
if (node.val.compareTo(val) > 0) {
node.leftNode = removeAssignVal(node.leftNode, val);
} else {
node.rightNode = removeAssignVal(node.rightNode, val);
}
Node resNode = node;
//更新高度;
resNode.height = Math.max(getHeight(resNode.leftNode),getHeight(resNode.rightNode))+1;
//维持平衡操作;
//极度偏左;
if (getHeightFactor(resNode) > 1 && getHeightFactor(resNode.leftNode) >= 0) {
//直接右旋;
resNode = RotateRight(resNode);
}
//极度偏右;
else if (getHeightFactor(resNode) < -1 && getHeightFactor(resNode.rightNode) <= 0) {
//直接左旋;
resNode = RotateLeft(resNode);
}
//左树先偏高,后面右子树偏高;
else if (getHeightFactor(resNode) > 1 && getHeightFactor(resNode.leftNode) < 0) {
//先左旋后右旋;
resNode.leftNode = RotateLeft(resNode.leftNode);
resNode = RotateRight(resNode);
}
//右树先偏高,后面左子树偏高;
else if (getHeightFactor(resNode) < -1 && getHeightFactor(resNode.rightNode) > 0) {
//先右旋再左旋;
resNode.rightNode = RotateRight(resNode.rightNode);
resNode = RotateLeft(resNode);
}
return resNode;
}
//中序遍历; 稍作修改,让这个遍历结果存入字符串;
public List<String> middleOrder() {
//若二叉树为空,则直接返回null空值;
if (root == null) {
return null;
}
//遍历的结果存入集合中;
List<String> list = new ArrayList<>();
middleOrder(root, list);
return list;
}
//中序遍历底层;
private void middleOrder(Node node, List<String> list) {
//递归结束点,若到达最后一层的叶子节点就停止;
if (node == null) {
return;
}
//中序遍历= 先遍历左子树 ==> 获取中间结点 ==> 遍历右子树
middleOrder(node.leftNode, list);
list.add(node.val + "<---高度因子--->" + getHeightFactor(node));
middleOrder(node.rightNode, list);
}
/**
* 输出打印树的中序遍历信息;
*/
@Override
public String toString() {
List<String> list = middleOrder();
list.forEach(a -> System.out.println(a + "\t"));
return "";
}
//查询元素;
public Node contains(T ele) {
if (root == null) {
return null;
}
return contains(root, ele);
}
//查询元素的底层;
private Node contains(Node root, T ele) {
//递归结束点;
if (root == null) {
return null;
}
//将当前根结点的值存储;
T val = root.val;
if (ele.compareTo(val) == 0) {
return root;
} else if (ele.compareTo(val) > 0) {
return contains(root.rightNode, ele);
} else {
return contains(root.leftNode, ele);
}
}
//删除最小节点;
public void removeMinNode() {
//找到最小元素;
T minNode = findMinNodeRecurve();
if (minNode == null) {
System.out.println("空树不用删除");
return;
}
System.out.println("删除的最小节点是=>" + minNode);
// 删除后的树的根结点挂到原树上;
root = removeMinNode(root);
this.size -= 1;
}
//删除最小节点的底层实现;
private Node removeMinNode(Node node) {
//若到达最左边,即停止;
if (node.leftNode == null) {
//右子树挂到删除节点处;
Node n = node.rightNode;
node.rightNode = null;
return n;
}
//递归;
node.leftNode = removeMinNode(node.leftNode);
return node;
}
//递归方式寻找最小元素;
public T findMinNodeRecurve() {
if (root == null) {
return null;
}
return findMinNodeRecurve(root).val;
}
//递归方式寻找最小元素的底层实现;
private Node findMinNodeRecurve(Node root) {
//递归结束点;
if (root.leftNode == null) {
return root;
}
return findMinNodeRecurve(root.leftNode);
}
/**
* 由当前根结点开始寻找指定的元素;
*
* @param node 根节点
* @param val 指定元素值
*/
private Node findAssignNode(Node node, T val) {
//没找到就返回null值;
if (node == null) {
return null;
}
//若当前结点就是指定的值;
if (node.val.compareTo(val) == 0) {
return node;
}
//当前的根结点比指定的值还大,根据二分搜索树性质,越小的 就在左子树去找;
else if (node.val.compareTo(val) > 0) {
//去左子树查询;
return findAssignNode(node.leftNode, val);
} else {
//排除上面的情况,就去右子树查找;
return findAssignNode(node.rightNode, val);
}
}
}
测试使用
//测试使用;
public static void main(String[] args) {
AVLStartTree<Integer> avlStartTree = new AVLStartTree<>();
Random random = new Random();
//添加元素;
avlStartTree.add(120);
for (int i = 0; i < 15; i++) {
avlStartTree.add(random.nextInt(1000));
}
//删除元素;
avlStartTree.removeAssignVal(120);
System.out.println("是否为二分搜索树->" + avlStartTree.isBSTTree());
System.out.println("是否为平衡树->" + avlStartTree.isAVLTree());
System.out.println(avlStartTree);
}
测试结果
是否为二分搜索树->true
是否为平衡树->true
60<---高度因子--->0
67<---高度因子--->0
100<---高度因子--->0
134<---高度因子--->0
147<---高度因子--->0
196<---高度因子--->-1
245<---高度因子--->0
348<---高度因子--->0
369<---高度因子--->0
382<---高度因子--->0
438<---高度因子--->-1
581<---高度因子--->0
771<---高度因子--->0
856<---高度因子--->-1
991<---高度因子--->0
删除方法优化
/**
* 删除方法优化;
* 删除指定数值;
* @param val 指定数值;
*/
public T removeAssignValOptimization(T val) {
if (root == null) {
System.out.println("空树不用删除");
return null;
}
//先去找是否存在; 要去新建方法;
Node node = findAssignNode(root, val);
//是否找到;
if (node != null) {
//删除后的剩余结点挂到根结点之后;
root = removeAssignValOptimization(root, val);
//元素个数减少;
this.size -= 1;
return node.val;
}
return null;
}
/**
* 删除方法优化;
* 删除指定结点的底层实现;在根结点为node的二分树中删除指定结点;
*
* @param node 指定根结点出发
* @param val 指定值
*/
private Node removeAssignValOptimization(Node node, T val) {
Node resNode = null;
//找到结点时;
if (node.val.compareTo(val) == 0) {
//第一种情况==> 该删除结点的左树为空;
if (node.leftNode == null) {
//删除当前的结点后;把原来后面的右子树挂到删了结点的位置;
Node RNode = node.rightNode;
node.rightNode = null;
resNode = RNode;
}
//第二种情况,右树为空;
else if (node.rightNode == null) {
//删除当前的结点后;把原来后面的左子树挂到删了结点的位置;
Node LNode = node.leftNode;
node.leftNode = null;
resNode = LNode;
} else {
//情况三; 左树 右树 都不为空时,可以选择找前驱结点(左子树那块区域的最大值) 或 后继结点(右子树那块区域的最小值)代替删除结点;
//这里选择找后继节点;
Node minR = findMinNodeRecurve(node.rightNode);
//调用;
Node minRNode = removeAssignValOptimization(node.rightNode,minR.val);
//后继节点放到删除的结点位置;
minR.leftNode = node.leftNode;
minR.rightNode = minRNode;
node.leftNode = null;
node.rightNode = null;
resNode = minR;
}
}
//递归;
//找结点时,若当前的根结点比指定的值还大,就去左边找; 否则去右边找;
else if (node.val.compareTo(val) > 0) {
node.leftNode = removeAssignValOptimization(node.leftNode, val);
resNode = node;
} else {
node.rightNode = removeAssignValOptimization(node.rightNode, val);
resNode = node;
}
//若要删除叶子节点;
if(resNode ==null){
return null;
}
//更新高度;
resNode.height = Math.max(getHeight(resNode.leftNode),getHeight(resNode.rightNode))+1;
Node finalNode = resNode;
//维持平衡操作;
//极度偏左;
if (getHeightFactor(resNode) > 1 && getHeightFactor(resNode.leftNode) >= 0) {
//直接右旋;
finalNode = RotateRight(resNode);
}
//极度偏右;
else if (getHeightFactor(resNode) < -1 && getHeightFactor(resNode.rightNode) <= 0) {
//直接左旋;
finalNode = RotateLeft(resNode);
}
//左树先偏高,后面右子树偏高;
else if (getHeightFactor(resNode) > 1 && getHeightFactor(resNode.leftNode) < 0) {
//先左旋后右旋;
resNode.leftNode = RotateLeft(resNode.leftNode);
finalNode = RotateRight(resNode);
}
//右树先偏高,后面左子树偏高;
else if (getHeightFactor(resNode) < -1 && getHeightFactor(resNode.rightNode) > 0) {
//先右旋再左旋;
resNode.rightNode = RotateRight(resNode.rightNode);
finalNode = RotateLeft(resNode);
}
return finalNode;
}