BEGAN: Boundary Equilibrium GAN
BeGan概览: DCGAN、WGAN、WGAN-GP、LSGAN、BEGAN原理总结及对比
BeGan解读: BEGAN解读
解读
BEGAN的主要贡献:
◆ 提出了一种新的简单强大GAN,使用标准的训练方式,不加训练trick也能很快且稳定的收敛
◆ 对于GAN中G,D的能力的平衡提出了一种均衡的概念(GAN的理论基础就是goodfellow理论上证明了GAN均衡点的存在,但是一直没有一个准确的衡量指标说明GAN的均衡程度)
◆ 提出了一种收敛程度的估计,这个机制只在WGAN中出现过 (一个总的loss来说明训练进度)。作者在论文中也提到,他们的灵感来自于WGAN,在此之前只有wgan做到了
简介
“我们希望研究匹配误差分布的效果,而不是直接匹配样本的分布”
以往,生成 以假乱真 的图片,需要G生成的数据分布 P g P_g Pg尽可能的接近真实数据 P x P_x Px的分布,因此,损失函数loss_fn去令G的生成数据分布 P g P_g Pg尽可能接近真实数据分布 P x P_x Px。比如:DCGAN、WGAN、WGAN-GP等等。
BEGAN不直接去估计生成分布Pg与真实分布Px的差距,进而设计合理的损失函数拉近他们之间的距离,而是估计分布的误差之间的距离.
作者认为只要分布的的误差分布相近的话,也可以认为这些分布是相近的。即如果我们认为两个人非常相似,又发现这两人中的第二个人和第三个人很相似,那么我们就完全可以说第一个人和第三个人长的很像。在BEGAN中,第一个人相当于训练的数据
x
x
x,第二个人相当于D对x编码解码后的图像
D
(
x
)
D(x)
D(x),第三个人相当于D以G的生成为输入的结果
D
(
g
(
z
)
)
D(g(z))
D(g(z)).
所以,如果
∣
∣
D
(
x
)
−
x
∣
∣
−
∣
∣
D
(
g
(
z
)
)
−
g
(
z
)
∣
∣
||D(x)-x|| - || D(g(z)) - g(z)||
∣∣D(x)−x∣∣−∣∣D(g(z))−g(z)∣∣不断趋近于0,那么随着训练,D(x)会不断接近x,那么D(g(z)) 接近于D(x),岂不是就意味着 g(z) 的数据分布和x分布几乎一样了,那么就说明G学到了生成数据的能力。
但是问题来了,如果
∣
∣
D
(
x
)
−
x
∣
∣
−
∣
∣
D
(
g
(
z
)
)
−
g
(
z
)
∣
∣
||D(x)-x|| - || D(g(z)) - g(z)||
∣∣D(x)−x∣∣−∣∣D(g(z))−g(z)∣∣刚好等于0,这时候,
D
(
x
)
D(x)
D(x)和
x
x
x可能还差的很远呢,那不就什么也学不到了。
结构图
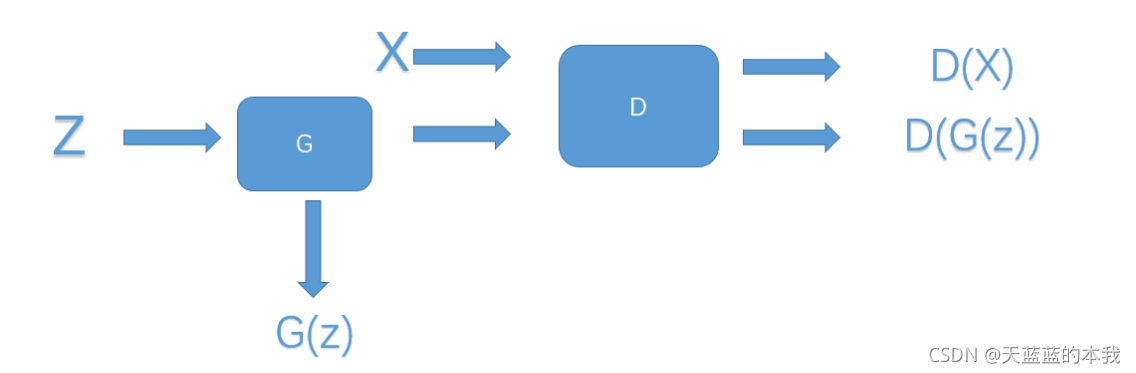
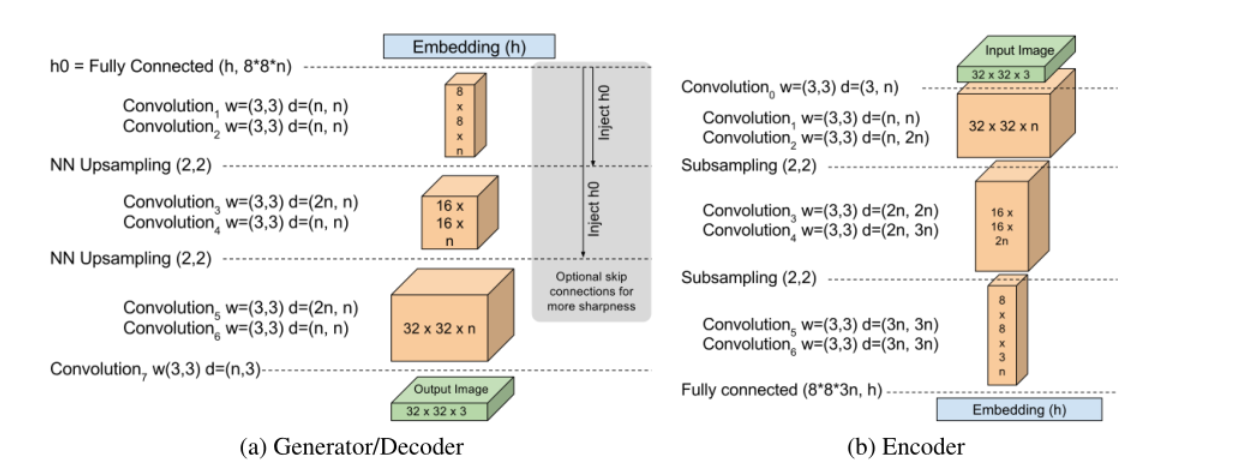
D使用auto-encoder结构,输入是图片,输出是经过编码解码后的图片.(如右图,论文中,生成器和鉴别器是一样的结构)
损失函数
D ( x ) − x D(x)-x D(x)−x是一个图片,假设图片上的每一个像素都满足独立同分布条件,根据中心极限定理,像素的误差近似满足正太分布。这时候我们就可以再用wassertein距离衡量距离。
先来看看论文
论文是这一篇《BEGAN: Boundary Equilibrium Generative Adversarial Networks》
自编码器(auto-encoder),也就是D网络。该网络的损失函数定义如下:
L
(
v
)
=
∣
v
−
D
(
v
)
∣
η
where
{
D
:
R
N
x
↦
R
N
x
is the autoencoder function.
η
∈
{
1
,
2
}
is the target norm.
v
∈
R
N
x
is a sample of dimension
N
x
\mathcal{L}(v)=|v-D(v)|^{\eta} \text { where } \begin{cases}D: \mathbb{R}^{N_{x}} \mapsto \mathbb{R}^{N_{x}} & \text { is the autoencoder function. } \\ \eta \in\{1,2\} & \text { is the target norm. } \\ v \in \mathbb{R}^{N_{x}} & \text { is a sample of dimension } N_{x}\end{cases}
L(v)=∣v−D(v)∣η where ⎩⎪⎨⎪⎧D:RNx↦RNxη∈{1,2}v∈RNx is the autoencoder function. is the target norm. is a sample of dimension Nx
此处的
L
(
v
)
L(v)
L(v)是一个pixel-wise的损失,表示真实输入图像
v
v
v和经过自编码网络D输出的
D
(
v
)
D(v)
D(v)的相似程度。
L
L
L越小,说明
v
和
D
(
v
)
v和D(v)
v和D(v)越相似。同理,
L
(
G
(
z
)
)
=
∣
G
(
z
)
−
D
(
G
(
z
)
)
∣
η
\mathcal L(G(z))=|G(z)-D(G(z))|^{\eta}
L(G(z))=∣G(z)−D(G(z))∣η,也是一个pixel-wise的损失,其中,
z
∈
[
−
1
,
1
]
N
z
z \in[-1,1]^{N_{z}}
z∈[−1,1]Nz,是维数为
N
z
{N_{z}}
Nz的均匀随机样本。
令
μ
1
,
2
\mu_{1,2}
μ1,2 是
L
L
L和
L
(
G
)
L(G)
L(G)的分布,
Γ
(
μ
1
,
μ
2
)
\Gamma\left(\mu_{1}, \mu_{2}\right)
Γ(μ1,μ2) 为
μ
1
\mu_{1}
μ1 和
μ
2
\mu_{2}
μ2的所有耦合集,
m
1
,
2
∈
R
m_{1,2} \in \mathbb{R}
m1,2∈R为它们各自的均值。则Wasserstein 距离可以表示为:
W
1
(
μ
1
,
μ
2
)
=
inf
γ
∈
Γ
(
μ
1
,
μ
2
)
E
(
x
1
,
x
2
)
∼
γ
[
∣
x
1
−
x
2
∣
]
W_{1}\left(\mu_{1}, \mu_{2}\right)=\inf _{\gamma \in \Gamma\left(\mu_{1}, \mu_{2}\right)} \mathbb{E}_{\left(x_{1}, x_{2}\right) \sim \gamma}\left[\left|x_{1}-x_{2}\right|\right]
W1(μ1,μ2)=γ∈Γ(μ1,μ2)infE(x1,x2)∼γ[∣x1−x2∣]
利用Jensen不等式(Jensen’s inequality),我们可以得到
W
1
(
μ
1
,
μ
2
)
W_{1}\left(\mu_{1}, \mu_{2}\right)
W1(μ1,μ2)下界(条件(1)) :
inf
E
[
∣
x
1
−
x
2
∣
]
⩾
inf
∣
E
[
x
1
−
x
2
]
∣
=
∣
m
1
−
m
2
∣
\inf \mathbb{E}\left[\left|x_{1}-x_{2}\right|\right] \geqslant \inf \left|\mathbb{E}\left[x_{1}-x_{2}\right]\right|=\left|m_{1}-m_{2}\right|
infE[∣x1−x2∣]⩾inf∣E[x1−x2]∣=∣m1−m2∣
鉴别器D的目标就是最大化
∣
m
1
−
m
2
∣
\left|m_{1}-m_{2}\right|
∣m1−m2∣。(为什么是这个目标?因为鉴别器的作用是分开真实图像
x
x
x和虚假图像
g
(
x
)
g(x)
g(x),并且查看经由本网络
D
(
x
)
D(x)
D(x)后的生成图
D
(
v
)
D(v)
D(v)和原图
v
v
v的
L
(
v
)
\mathcal{ L }(v)
L(v),那么,为了编码尽量靠近原图,应该让
L
(
x
)
\mathcal{ L }(x)
L(x)尽可能小,即:
L
(
x
)
\mathcal{ L }(x)
L(x)取正值; 为了区分虚假图像,应该让
L
(
g
(
x
)
)
\mathcal{ L }(g(x))
L(g(x)) 尽可能大,即:
L
(
g
(
x
)
)
\mathcal{ L }(g(x))
L(g(x))取负值)。 因为最小化
m
1
m_1
m1自然会导致对真实图像的自动编码,故论文方案是
{
W
1
(
μ
1
,
μ
2
)
⩾
m
2
−
m
1
m
1
→
0
m
2
→
∞
\left\{\begin{array}{l}W_{1}\left(\mu_{1}, \mu_{2}\right) \geqslant m_{2}-m_{1} \\ m_{1} \rightarrow 0 \\ m_{2} \rightarrow \infty\end{array}\right.
⎩⎨⎧W1(μ1,μ2)⩾m2−m1m1→0m2→∞ ,抛弃了与之相反的另一种最大化倾向。
继续解读(下面大都是博客里的解读)
L L L和 L ( G ) L(G) L(G)都是pixel-wise的, L L L和 L ( G ) L(G) L(G)的数值一定满足某种分布,在有足够大的像素的情况下,假设独立同分布条件,那么,根据中心极限定理,像素的误差近似满足正太分布。令 L ( v ) {L}(v) L(v)和 L ( G ) L(G) L(G)两个损失函数的分布,分别是 µ 1 = N ( m 1 ; C 1 ) µ1 = N(m1; C1) µ1=N(m1;C1) 和 µ 2 = N ( m 2 ; C 2 ) µ2 = N(m2; C2) µ2=N(m2;C2) 的正太分布, m m m为均值,维度为 R p Rp Rp, c c c为方差维度为 R p × p Rp×p Rp×p。
那么根据wassertein公式,两个正太分布µ1、µ2的距离为:
W
(
μ
1
,
μ
2
)
2
=
∥
m
1
−
m
2
∥
2
2
+
trace
(
C
1
+
C
2
−
2
(
C
2
1
/
2
C
1
C
2
1
/
2
)
1
/
2
)
W\left(\mu_{1}, \mu_{2}\right)^{2}=\left\|m_{1}-m_{2}\right\|_{2}^{2}+\operatorname{trace}\left(C_{1}+C_{2}-2\left(C_{2}^{1 / 2} C_{1} C_{2}^{1 / 2}\right)^{1 / 2}\right)
W(μ1,μ2)2=∥m1−m2∥22+trace(C1+C2−2(C21/2C1C21/2)1/2)
其中,trace是求迹操作,P=1时,简化为: W ( μ 1 , μ 2 ) 2 = ∥ m 1 − m 2 ∥ 2 2 + ( c 1 + c 2 − 2 c 1 c 2 ) W\left(\mu_{1}, \mu_{2}\right)^{2}=\left\|m_{1}-m_{2}\right\|_{2}^{2}+\left(c_{1}+c_{2}-2 \sqrt{c_{1} c_{2}}\right) W(μ1,μ2)2=∥m1−m2∥22+(c1+c2−2c1c2)
作者就开始研究,是否上式的第一项就足以优化W2,答案是肯定的,只要满足以下条件:
c
1
+
c
2
−
2
c
1
c
2
∥
m
1
−
m
2
∣
2
2
\frac{c_{1}+c_{2}-2 \sqrt{c_{1} c_{2}}}{\| m_{1}-\left.m_{2}\right|_{2} ^{2}}
∥m1−m2∣22c1+c2−2c1c2 i s constant or monotonically increasing w.r.
W
W
W
而且,满足条件(1)情况下,问题就简化为:
W ( μ 1 , μ 2 ) 2 ∝ ∥ m 1 − m 2 ∥ 2 2 W\left(\mu_{1}, \mu_{2}\right)^{2} \propto\left\|m_{1}-m_{2}\right\|_{2}^{2} W(μ1,μ2)2∝∥m1−m2∥22 , 即 W ( μ 1 , μ 2 ) 2 W\left(\mu_{1},\mu_{2}\right)^{2} W(μ1,μ2)2 和 ∥ m 1 − m 2 ∥ 2 2 \left\|m_{1}-m_{2}\right\|_{2}^{2} ∥m1−m2∥22成正比。
对比WGAN就可以发现,这里不需要lipschize限制,这时,我们就可以给GAN分配任务了,令D不断的最大化 m 2 m2 m2(即 v − G ( v ) 的 均 值 v-G(v)的均值 v−G(v)的均值), 最小化 m 1 m1 m1(即 v − D ( v ) 的 均 值 v-D(v)的均值 v−D(v)的均值),而G则不断最小化 m 2 m2 m2,当m2 接近m1的时候我们就认为GAN完成了训练。
生成器Loss和判别器Loss
{ L D = L ( x ) − k t ⋅ L ( G ( z D ) ) for θ D L G = L ( G ( z G ) ) for θ G k t + 1 = k t + λ k ( γ L ( x ) − L ( G ( z G ) ) ) for each training step t \begin{cases}\mathcal{L}_{D}=\mathcal{L}(x)-k_{t} \cdot \mathcal{L}\left(G\left(z_{D}\right)\right) & \text { for } \theta_{D} \\ \mathcal{L}_{G}=\mathcal{L}\left(G\left(z_{G}\right)\right) & \text { for } \theta_{G} \\ k_{t+1}=k_{t}+\lambda_{k}\left(\gamma \mathcal{L}(x)-\mathcal{L}\left(G\left(z_{G}\right)\right)\right) & \text { for each training step } t\end{cases} ⎩⎪⎨⎪⎧LD=L(x)−kt⋅L(G(zD))LG=L(G(zG))kt+1=kt+λk(γL(x)−L(G(zG))) for θD for θG for each training step t
L ( x ) = ∣ x − D ( x ) ∣ η L(x)=|x-D(x)|^{\eta} L(x)=∣x−D(x)∣η
L ( G ( z ) ) = ∣ G ( z ) − D ( G ( z ) ) ∣ η L(G(z))=|G(z)-D(G(z))|^{\eta} L(G(z))=∣G(z)−D(G(z))∣η
{ η ∈ { 1 , 2 } is the target norm. \begin{cases}\eta \in\{1,2\} & \text { is the target norm. } \\ \end{cases} {η∈{1,2} is the target norm.
z D z_{D} zD and z G z_{G} zG 采样自 z z z , k 0 = 0 , λ k = 0.001 k_0=0,\lambda_k = 0.001 k0=0,λk=0.001,
改进及总loss
从以上分析的结果来看,只要按步骤优化损失函数,就能完成GAN的训练,但是还没有那么简单,或许也注意到,为什么论文的名字叫做Boundary Equilibrium GAN,到这里完全没有涉及到Boundary Equilibrium的概念,我们继续分析。
GAN完成训练时的结果是什么样子的,理想情况下肯定是m1=m2的时候是最好的,即:
E
[
L
(
x
)
]
=
E
[
L
(
G
(
z
)
)
]
\mathbb{E}[\mathcal{L}(x)]=\mathbb{E}[\mathcal{L}(G(z))]
E[L(x)]=E[L(G(z))]
分布的期望相等,那就是G产生的图片和真实图像分布相同,这时出现了一个问题,
m
1
=
m
2
m1=m2
m1=m2条件下,条件1不 再是一个不可忽略项,反而趋近于无穷,作者为了解决这个问题,特意加入了一个超参数,
γ
\gamma
γ 取值
[
0
,
1
]
[0 ,1]
[0,1] 之间定义:
γ
=
E
[
L
(
G
(
z
)
)
]
E
[
L
(
x
)
]
37
\gamma=\frac{\mathbb{E}[\mathcal{L}(G(z))]}{\mathbb{E}[\mathcal{L}(x)]_{37}}
γ=E[L(x)]37E[L(G(z))]
鉴别器有两个目标: 编码真实图像 和 区分真实图像与生成图像 ,
γ
\gamma
γ让我们平衡这两个目标,并且,
γ
\gamma
γ越大,生成图像的多样性就越好。
有了这个限制,就不会出现m1=m2的情形了, 这就相当于一个boundary 将均衡条件限制住了, 这就是论文名 字的由来。
另外一个重要的参数就是Mgloable了,形式如下:
M
g
l
o
b
a
l
=
L
(
x
)
+
∣
γ
L
(
x
)
−
L
(
G
(
z
G
)
)
∣
\mathcal{M}_{g l o b a l}=\mathcal{L}(x)+\left|\gamma \mathcal{L}(x)-\mathcal{L}\left(G\left(z_{G}\right)\right)\right|
Mglobal=L(x)+∣γL(x)−L(G(zG))∣
实验
参数设置:
batch_size = 16
BEGAN的训练结果:不同的
γ
γ
γ, 可以在图片的质量和生成多样性之间做选择。

大部分情况来说,还是wgan-gp用的更多一些。生成高清图像BEGAN最简单合适。
论文idea
GAN ,一个生成器,2个鉴别器
生成器,可以使用 <paper01 感知一致> 中的,它的生成图像
I
f
I_f
If效果很好
鉴别器,使用中的,它使用了2个鉴别器
大体思路是:
让鉴别器 D v D_v Dv,去使得 I f I_f If和 I v I_v Iv尽可能靠近
让鉴别器 D r D_r Dr,去使得 I f I_f If和 I r I_r Ir尽可能靠近
考虑到他和本论文的不同:
本论文的输入是噪音z
待实现的输入是 I v I_v Iv和 I r I_r Ir
相同之处: D的鉴别图像都是真实图像。
查了一下,已经有了一篇
《LBP-BEGAN:GAN for 图像融合》
如何深入
他使用的是LBP损失函数,这个可以改,甚至可以加在名字里
此外:
他使用了Dense,有没有将红外连接到各层呢?
他使用的是不是双鉴别器呢?在看了。
