文章 链接 对几种不同类型的微分做了很详细的图文说明，值得一看

Tensorflow 求解梯度（微分）的核心函数代码分析如下

@tf_export(v1=["gradients"])
def gradients(ys,
              xs,
              grad_ys=None,
              name="gradients",
              colocate_gradients_with_ops=False,
              gate_gradients=False,
              aggregation_method=None,
              stop_gradients=None,
              unconnected_gradients=UnconnectedGradients.NONE):
'''
  Args:
    ys: A `Tensor` or list of tensors to be differentiated.
    xs: A `Tensor` or list of tensors to be used for differentiation.
    grad_ys: Optional. A `Tensor` or list of tensors the same size as
      `ys` and holding the gradients computed for each y in `ys`.
  ...
  Returns:
    A list of `sum(dy/dx)` for each x in `xs`.
'''
  ...
  with ops.get_default_graph()._mutation_lock():
    return gradients_util._GradientsHelper(
        ys, xs, grad_ys, name, colocate_gradients_with_ops,
        gate_gradients, aggregation_method, stop_gradients,
        unconnected_gradients)

tf.gradients 计算 tensor list ys 对 tensor list xs 的梯度，计算梯度的len和xs一样，计算结果是对于每个   求出   (其中 ) ，换而言之即遍历xs，每取出1个xi，把ys中每个tensor对xi求梯度然后相加作为ys对xi的梯度结果，最后计算出ys对所有的xi的梯度，组成ys对xs的梯度结果

计算梯度的核心函数_GradientsHelper 分析如下

def _GradientsHelper(ys,
                     xs,
                     grad_ys=None,
                     name="gradients",
                     colocate_gradients_with_ops=False,
                     gate_gradients=False,
                     aggregation_method=None,
                     stop_gradients=None,
                     unconnected_gradients=UnconnectedGradients.NONE,
                     src_graph=None):
  """Implementation of gradients()."""
...
    # The approach we take here is as follows: Create a list of all ops in the
    # subgraph between the ys and xs.  Visit these ops in reverse order of ids
    # to ensure that when we visit an op the gradients w.r.t its outputs have
    # been collected.  Then aggregate these gradients if needed, call the op's
    # gradient function, and add the generated gradients to the gradients for
    # its input.

    # Initialize the pending count for ops in the connected subgraph from ys
    # to the xs.
    to_ops = [t.op for t in ys]
    from_ops = [t.op for t in xs]
    stop_gradient_ops = [t.op for t in stop_gradients]
    reachable_to_ops, pending_count, loop_state = _PendingCount(
        to_ops, from_ops, colocate_gradients_with_ops, func_graphs, xs_set)

    # Iterate over the collected ops.
    #
    # grads: op => list of gradients received on each output endpoint of the
    # op.  The gradients for each endpoint are initially collected as a list.
    # When it is time to call the op's gradient function, for each endpoint we
    # aggregate the list of received gradients into a Add() Operation if there
    # is more than one.
    grads = {}

    # Add the initial gradients for the ys.
    for y, grad_y in zip(ys, grad_ys):
      _SetGrad(grads, y, grad_y)

    # Initialize queue with to_ops.
    queue = collections.deque()
    # Add the ops in 'to_ops' into the queue.
    to_ops_set = set()
    for op in to_ops:
      # 'ready' handles the case where one output gradient relies on
      # another output's gradient.
      ready = (pending_count[op] == 0)
      if ready and op not in to_ops_set and op in reachable_to_ops:
        to_ops_set.add(op)
        queue.append(op)
...
    while queue:
      # generate gradient subgraph for op.
      op = queue.popleft()
...
        if has_out_grads and (op not in stop_ops):
          try:
            grad_fn = ops.get_gradient_function(op)
...
          with ops.name_scope(op.name + "_grad"):
            # pylint: disable=protected-access
            with src_graph._original_op(op):
              # pylint: enable=protected-access
              if grad_fn:
                # If grad_fn was found, do not use SymbolicGradient even for
                # functions.
                in_grads = _MaybeCompile(grad_scope, op, func_call,
                                         lambda: grad_fn(op, *out_grads))
              else:
                # For function call ops, we add a 'SymbolicGradient'
                # node to the graph to compute gradients.
                in_grads = _MaybeCompile(grad_scope, op, func_call,
                                         lambda: _SymGrad(op, out_grads))
...
          _LogOpGradients(op, out_grads, in_grads)
...
      # Update pending count for the inputs of op and enqueue ready ops.
      _UpdatePendingAndEnqueueReady(grads, op, queue, pending_count, loop_state,
                                    xs_set)

...
  return [_GetGrad(grads, x, unconnected_gradients) for x in xs]

核心逻辑包括

• _PendingCount 将计算图中ys和xs之间的子图构建一个“可以到达”的op list reachable_to_ops，反向遍历这个list（反向传播），确保每个被遍历的OP，它的所有输出梯度已经计算出来了；注意：这里的梯度其实是指该OP的outputs 相对ys的梯度，如果ys是整个模型的Loss，那么即是d(Loss)/d(OP'outputs) 
  • _PendingCount还对ys和xs之间子图的每个OP的input tensor创建该input 对应OP的pending_count计算，换而言之即统计了ys和xs之间子图的每个OP在反向传播过程计算梯度的过程中输入的个数有几个

  • def _PendingCount(to_ops, from_ops, colocate_gradients_with_ops, func_graphs,
                      xs_set):
    ...  
    # Initialize pending count for between ops.
      pending_count = collections.defaultdict(int)
      for op in between_op_list:
        for x in _NonEagerInputs(op, xs_set):
          if x.op in between_ops:
            pending_count[x.op] += 1

  • pending_count的字面解释比较难以理解，可以用下图说明，即xs和ys之间的子图有4个OP，那么从最后一个OP4开始遍历，它的input tensor对应的OP 即OP2和OP3的pending_count[OP2]为1，pending_count[OP3]为1，而OP2和OP3的input tensor都对应OP1，所以pending_count[OP1]为2
  • 这样就可以知道，在反向创建计算梯度的过程中，OP2 OP3的梯度输入个数为1，OP1的梯度输入个数为2 （OP在正向传播的输出，即反向传播的输入）

 

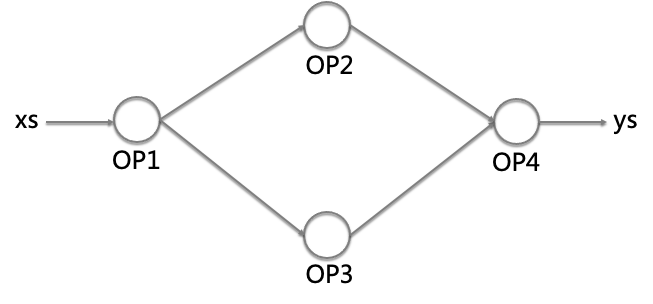
• 两个重要变量开始在代码逻辑中起作用
  • 一个队列queue，队列里存放计算图里所有出度为0的OP，其实就是该OP的所有输出相对ys的梯度已经都计算出来的OP，循环遍历该queue，取出OP来计算该OP的输入相对于ys的梯度
  • 一个字典grads，字典的键是操作符本身，值是该操作符每个输出端收到的梯度列表
  • queue首先放入的是ys的OP，比如上图的OP4，它一定是ready的（它的梯度输入比如是 d(ys)/d(ys) = 1 一定是已经计算出来了）
• 通过找出OP对应的梯度计算函数 grad_fn，计算OP的输入相对ys的梯度，保存都grads

• ​注意每个函数都使用了装饰器RegisterGradient包装，对有m个输入，n个输出的操作符，相应的梯度函数需要传入两个参数
  • 操作符本身
  • n个张量对象，代表OP每个输出相对ys的梯度
  • 返回m个张量对象，代表OP每个输入相对ys的梯度
  • 大部分操作符的梯度计算方式已经由框架给出，但是也可以自定义操作和对应的梯度计算函数

@ops.RegisterGradient("Log")
  def _LogGrad(op, grad):
    """Returns grad * (1/x)."""
    x = op.inputs[0]
    with ops.control_dependencies([grad]):
      x = math_ops.conj(x)
      return grad * math_ops.reciprocal(x)

• _LogOpGradients(op, out_grads, in_grads) 可以通过python log 打印OP的输出相对ys的梯度以及经过grad_fn计算出来的OP的输入相对ys的梯度，使用方法可以参考我的另外一篇文章
• _UpdatePendingAndEnqueueReady 函数更新OP的pending_count，如果pending_count[op]==0，即表示一个OP的所有输出相对ys的梯度已经都计算出来了，那么这个OP就可以加入queue中，去计算该OP的输入相对ys的梯度，即反向传播过程的计算
• 最后返回grads中保存的ys对xs的梯度计算结果

​