本文介绍 LeetCode 题集中，有关深度优先搜索（DFS）和广度优先搜索（BFS）的问题。

110. Balanced Binary Tree（平衡二叉树）

问题描述

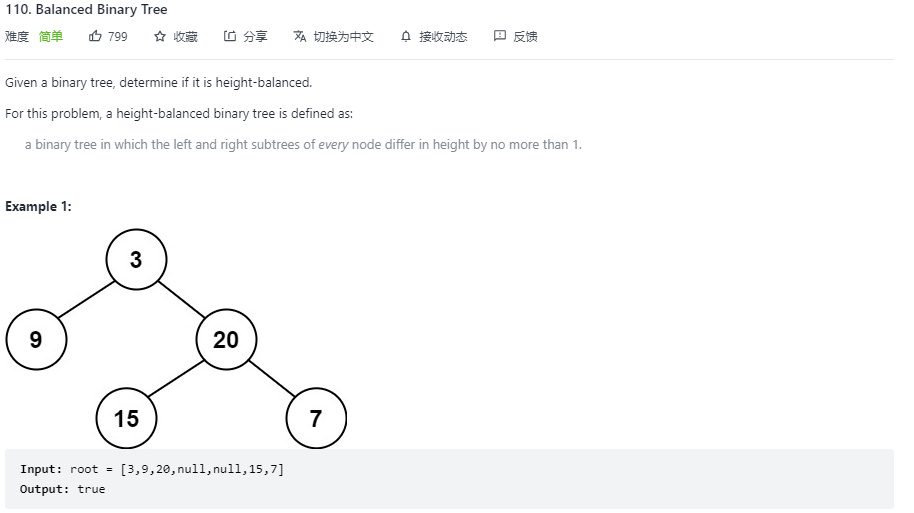
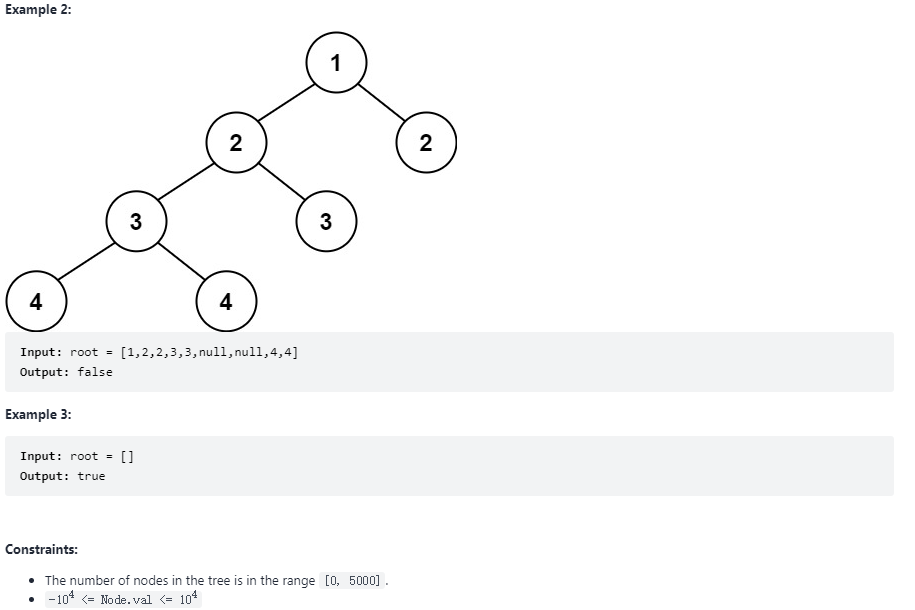
思路与代码

本题可采用深度优先搜索的方法，遍历每一个子节点下是否为平衡树，输出最终结果。

代码如下：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        def run(root: TreeNode) -> bool:
            def get_depth(root: TreeNode):
                if not root:
                    return 0
                else:
                    return max(get_depth(root.left), get_depth(root.right)) + 1

            if not root:
                return True

            # not balanced
            if abs(get_depth(root.left) - get_depth(root.right)) > 1:
                return False

            return run(root.left) and run(root.right)

        return run(root=root)

运行效果：

效果有些不理想，这里提出一种优化方案。由于只要有一个子节点下为不平衡树，整体即为不平衡树，因此可以在获取深度时即做剪枝。

代码如下：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        def run(root: TreeNode) -> bool:  # 返回 -1 即为提前剪枝
            def get_depth(root: TreeNode):
                if not root:
                    return 0
                
                lh = get_depth(root.left)
                if lh == -1:
                    return -1
                rh = get_depth(root.right)
                if rh == -1:
                    return -1

                if abs(lh - rh) > 1:
                    return -1

                return max(lh, rh) + 1

            if not root:
                return True

            return get_depth(root) != -1

        return run(root=root)

运行效果：

111. Minimum Depth of Binary Tree（二叉树的最小深度）

问题描述

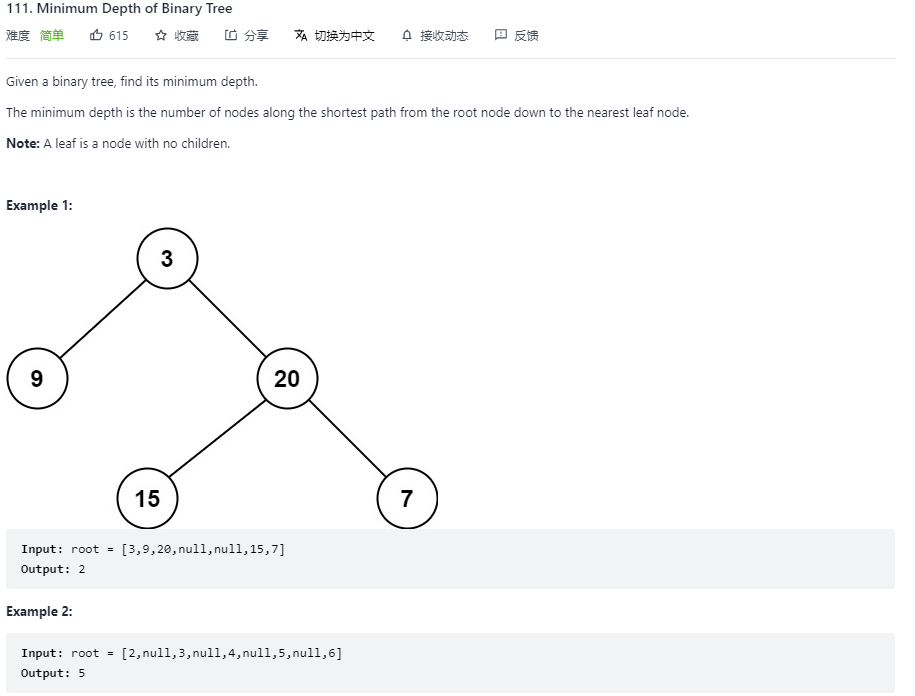
思路与代码

关于本题，介绍深度优先搜索和广度优先搜索两种思路。

深度优先搜索（DFS）

深度优先搜索采用递归的方式实现。

代码如下：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        def run(root: TreeNode) -> int:
            if not root:
                return 0

            ld = run(root.left)
            rd = run(root.right)

            if not ld:
                return rd + 1
            elif not rd:
                return ld + 1

            return min(ld, rd) + 1

        return run(root=root)

运行结果：

广度优先搜索（BFS）

广度优先搜索采用队列的数据结构实现，此处采用 Python 语言的 list 数据类型模拟队列的操作。

代码如下：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0

        list_queue = []
        list_queue.append(root)
        min_depth = 1
        cur_size = 0
        while list_queue:
            cur_size = len(list_queue)
            
            for i in range(cur_size):
                # pop the head of queue
                node = list_queue[0]
                list_queue = list_queue[1:]

                # no child nodes
                if not node.left and not node.right:
                    return min_depth

                # add child nodes to queue
                if node.left:
                    list_queue.append(node.left)
                if node.right:
                    list_queue.append(node.right)

            min_depth += 1

        return min_depth

运行效果：