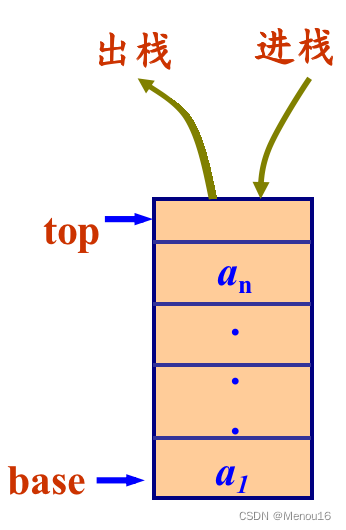
栈和队列都是特殊的线性表,因此定义栈和队列与之前的线性表异曲同工:
顺序栈
顺序栈的架构

顺序栈的特点
top=0 或top=base 表示空栈
base=NULL表示栈不存在
当插入新的栈顶元素时,指针top+1
删除栈顶元素时,指针top-1
当top>stacksize时,栈满,溢出
注意,此处的top栈顶指针是指向栈顶元素的下一个元素,也有一种说法是指向栈顶元素,两种都可,此处采用前者
1、创建栈
或
typedef int SElemType;
typedef struct{
SElemType data[MAXSIZE];
int top;//栈顶指针
}或使用STL库的栈

头文件#include <stack>
关于入栈操作
Status Push(SqStack *S,SElemType e){
if(S->top == MAXSIZE-1){
return ERROR;
}
S->top++;
S->data[S->top]==e;
return ok;
} 
或者

关于出栈操作
可以
Status Pop(SqStack *S, SElemType *e){
if(S->top==-1)
return ERROR;
*e=S->data[S->top];
S->top--;
return OK;
}
或者

亦或者

这里是先打印再弹出
判栈满的函数

用STL栈无法实现栈满的监测,因为STL栈没有栈满这个概念。
链栈
我们知道栈顶是一个栈做压入和弹出的地方,而链表形态下也拥有一个头指针,那么我们就可以利用头指针作为栈顶指针,对于链栈而言,因为栈顶是在链表头部,因此不存在栈满的情况(除非内存已满)
对于链栈而言,它和链表空的条件一样,就是头指针(栈顶指针)top==NULL
栈的应用【编程】递归
说到递归,著名的斐波拉契数列就是一个递归数列,而斐波拉契数就是指符合斐波拉契数列运算方式得来的数。
上图就是斐波拉契数列的原理,可以看到,除了0,1之外,斐波拉契数列的n项等于n-1和n-2项之和。直观实现特定位数的斐波拉契数列的程序在上面。但是不够简洁,不能提现斐波拉契的精髓
看看修改过的程序:
#include<iostream>
using namespace std;
int Feibo(int i){
if(i<2)
return i == 0?0:1;
return Feibo(i-1)+Feibo(i-2);
}
int main(){
int n=0;
cin>>n;
cout<<Feibo(n)<<endl;
return 0;
}
/Users/yuwenao/untitled12/cmake-build-debug-/untitled12
9
34
进程已结束,退出代码为 0
实现了,优美的递归运用,通过三行代码实现feibo。而递归是🈶️编译器使用栈来实现的。
栈的第二个应用——四则运算求值
后缀表示法转换
为了解决四种运算在一条式子处理的先后次序而发明的算法
例如: 9 +(3-1)* 3+ 10 / 2 这一条表达式,
化为后缀表达式:9 3 1 - 3 * + 10 2 / + 去掉了括号,那么如何编写程序处理这种式子呢?
规则:遇到数字则入栈,遇到运算符就将栈顶两数字出栈并对应运算
如上式,第一步:9、3、1入栈
第二步:读取到“-”号,3、1出栈,运算“3-1”,得2,2入栈
第三步:读3入栈
第四步:读取到“*”,3、2出栈,运算“2*3”,得6入栈
第五步:读取到+号,6、9出栈,运算9+6=15,15入栈
第六步:10入栈;
第七步:2入栈;
第八步:读取到/,10、2出栈,运算10/2=5入栈;
最后一步:读到+号,15、5出栈,运算15+5=20入栈
20出栈,栈空,将结果输出,运算结束。
我们了解了后缀表示法到式子的运算原理,我们开始实际应用,第一步:我们如何编写将中缀表达式转化为后缀表达式的程序呢?
规则:从左到右遍历整个表达式,若是数字就输出,若是符号,则比较与栈顶符号的优先级,如果是右括号或者优先级不高于栈顶符号则栈顶符号依次输出,最后将符号入栈,依次类推。
例如上边的表达式:9 +(3-1)* 3+ 10 / 2
第一步:读取到9,输出,读取到+,入栈
第二步:读到左括号,比较和+号到优先级,因为左括号还未配对优先级低,入栈
第三步:读取3,输出,读取-号,比(的优先级高,入栈;
第四部:读取1,入栈,读取到右括号),由于右括号优先级最高,因此弹出栈顶元素“-”,依次出栈,直到弹出左括号为止。之后是*号,因为*号优先级高于+,因此入栈
第五步:读取3,输出,读取+号,因为+号优先级低于*,因此*输出,而因为没有比+优先级更低的符号了,因此+也出栈(现在是全部出栈),随后这个“+”入栈,至此,有:9 3 1 - 3 * +被输出。
第六步:读取10,输出,读取/,因为/比+优先级高,因此入栈,再读取2,输出
第七步:式子读取完毕,剩余符号依次出栈:10 2 / +,现在输出为:9 3 1 - 3 * + 10 2 / +
结束,转换完成。
呼,意外的多,下篇是队列