⭐️前面的话⭐️
大家好!本篇文章将介绍的剑指offerOJ题,来自力扣[剑指 Offer 55 - II. 平衡二叉树]题解,本文将以二叉树的概念以及二叉树深度为基础,以该题为背景介绍平衡二叉树,展示代码语言暂时为:Java,C/C++。
📒博客主页:未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创,CSDN首发!
📆首发时间:🌴2021年12月23日🌴
✉️坚持和努力一定能换来诗与远方!
💭刷题推荐书籍:📚《剑指offer专项版》,📚《剑指offer第2版》
💬参考在线编程网站:🌐牛客网🌐力扣
博主的码云gitee,平常博主写的程序代码都在里面。
博主的github,平常博主写的程序代码都在里面。
🙏作者水平很有限,如果发现错误,一定要及时告知作者哦!感谢感谢!
📌导航小助手📌
- ⭐️剑指 Offer 55 - II. 平衡二叉树⭐️
- 🔐题目详情
- 💡解题思路
- 🔑源代码
- 🌱总结

⭐️剑指 Offer 55 - II. 平衡二叉树⭐️
🔐题目详情
输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
示例:
给定二叉树 [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
返回 true。
给定二叉树 [1,2,2,3,3,null,null,4,4]
1
/ \
2 2
/ \
3 3
/ \
4 4
返回 false 。
| 来源:力扣(LeetCode)链接:剑指 Offer 55 - II. 平衡二叉树 |
|---|
💡解题思路
预备知识:
数据结构之树,树的深度及二叉树深度求法,二叉树,平衡二叉树,前三点已经在博文剑指 Offer 55 - I. 二叉树的深度介绍过了,这里就不多赘述了。
问题:什么是平衡二叉树?
如果二叉树的任意结点都满足其左右子树的深度之差不超过1,则该二叉树为平衡二叉树。
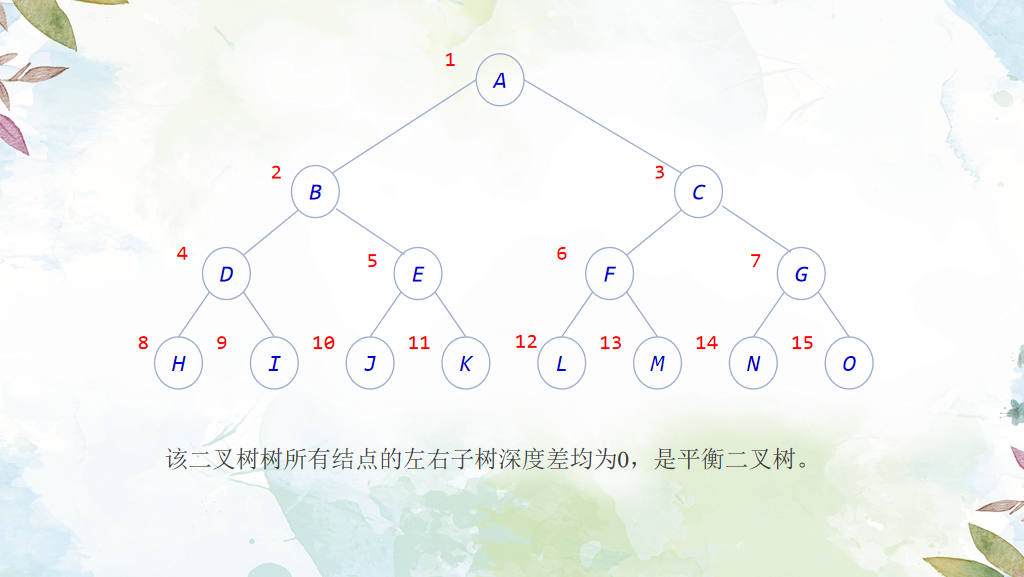
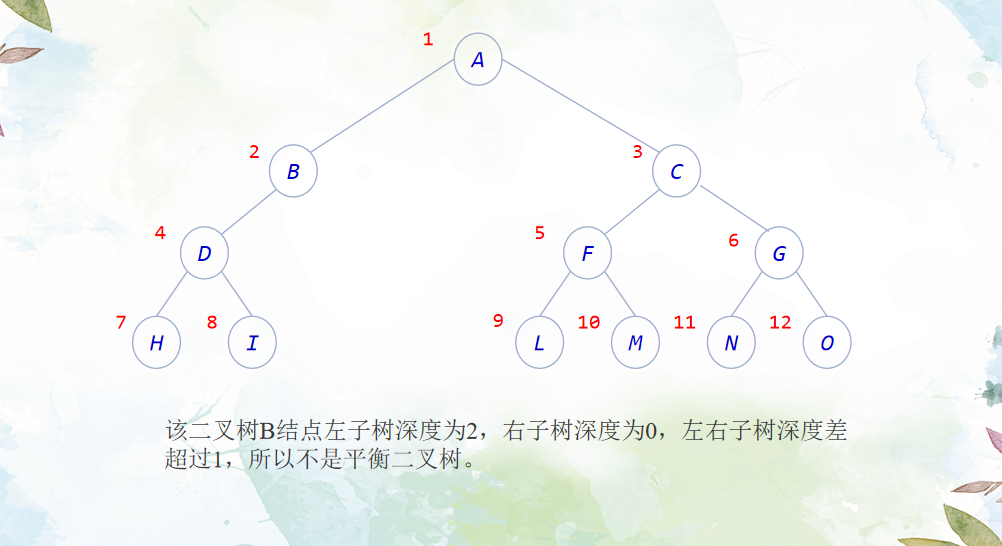
解题思路:
从根结点开始,判断所有的结点的左右子树的深度差是否小于1,满足此条件返回true,否则返回false,如果结点为null,返回true。
从二叉树中单个某子树结点看,此结点的左右子树深度差不大于1,并且该结点的左右子树的根结点也满足其子树深度差不大于1,这样就能确定该二叉树是平衡二叉树。
🔑源代码
Java:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int maxDeep(TreeNode subtree) {
if (subtree == null) {
return 0;
}
return 1 + Math.max(maxDeep(subtree.left), maxDeep(subtree.right));//求深度
}
public boolean isBalanced(TreeNode root) {
if (root == null) {
return true;
}
int ret = Math.abs(maxDeep(root.left) - maxDeep(root.right));
if (ret <= 1 && isBalanced(root.left) && isBalanced(root.right)) {
return true;//判断平衡二叉树
}
return false;
}
}
C:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
int max(int a, int b)
{
return a > b ? a : b;
}
int maxDeep(struct TreeNode* subtree)
{
if (subtree == NULL)
{
return 0;
}
return 1 + max(maxDeep(subtree->left), maxDeep(subtree->right));
}
bool isBalanced(struct TreeNode* root){
if (root == NULL)
{
return true;
}
int ret = fabs(maxDeep(root->left) - maxDeep(root->right));
if (ret <= 1 && isBalanced(root->left) && isBalanced(root->right))
{
return true;
}
return false;
}
C++:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int maxDeep(TreeNode * subtree) {
if (subtree == NULL) {
return 0;
}
return 1 + max(maxDeep(subtree->left), maxDeep(subtree->right));
}
bool isBalanced(TreeNode* root) {
if (root == NULL) {
return true;
}
int ret = abs(maxDeep(root->left) - maxDeep(root->right));
if (ret <= 1 && isBalanced(root->left) && isBalanced(root->right)) {
return true;
}
return false;
}
};
🌱总结
从根结点开始,判断所有的结点的左右子树的深度差是否小于1,满足此条件返回true,否则返回false,如果结点为null,返回true。
类似题如下:
110. 平衡二叉树

