栈

栈的定义和特点

栈(stack) 是限定仅在表尾进行插入或删除操作的线性表，表尾—栈顶（Top），表头—栈底（Base），不含元素的空表称空栈。

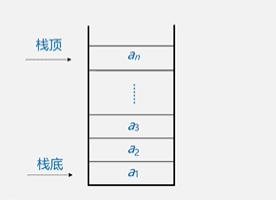
特点：先进后出(FILO)或后进先出(LIFO)

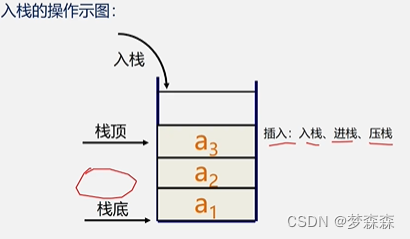
入栈： 插入元素到栈顶(即表尾)的操作

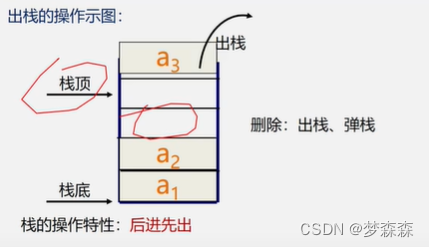
出栈： 从栈顶(即表尾)删除最后一个元素的操作

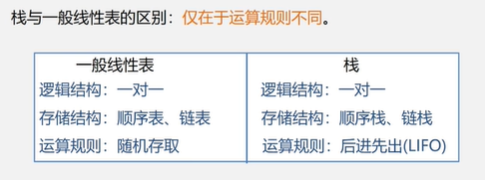
栈与一般线性表的区别

栈的抽象数据类型定义：

ADT Stack {
      数据对象：
         D＝{ ai | ai ∈SElemSet, i=1,2,...,n,  n≥0 }
      数据关系：
         R1＝{ <ai-1, ai >| ai-1, ai∈D, i=2,...,n }
                   约定an 端为栈顶，a1 端为栈底。 
      基本操作：初始化、进栈、出栈、取栈顶元素等
} ADT Stack

顺序栈的表示和实现

顺序栈的表示

  #define  STACK_INIT_SIZE  100; 
  #define  STACKINCREMENT   10;  
  typedef struct {
     SElemType  *base;     //栈底指针 
     SElemType  *top;    // 栈顶指针
     int  stacksize;    //最大容量
  } SqStack;

顺序栈的实现

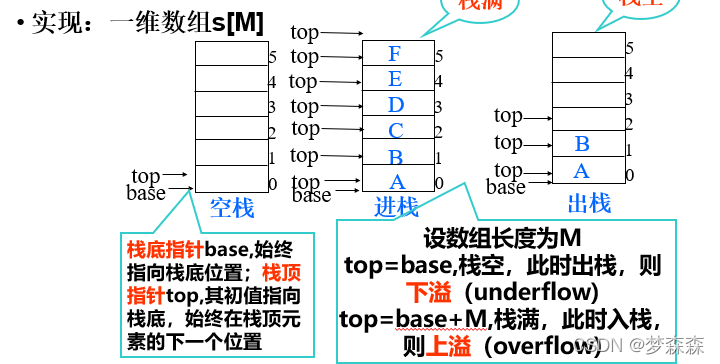
栈满时的处理方法：
1、报错,返回操作系统
2、分配更大的空间，作为栈的存储空间，将原栈的内容移入新栈。

顺序栈的初始化

Status InitStack (SqStack &S){// 构造一个空栈S
   S.base=(SElemType*)malloc(STACK_INIT_SIZE*  
                                       sizeof(SElemType));
   if (!S.base) exit (OVERFLOW); //存储分配失败
   S.top = S.base;
   S.stacksize = STACK_INIT_SIZE;
   return OK;
}

清空顺序栈（ClearStack）:

Status ClearStack(SqStack s){
	if(S.base) S.top = S.base;
	return OK;

销毁顺序栈（DestroyStack):

Status DestroyStack(Sqstack &s){
	if(S.base){
		delete S.base;
		S.stacksize = 0;
		S.base =S.top = NULL;}
		return OK;
}

顺序栈的入栈(Push):

Status Push (SqStack &S, SElemType e) {
   if (S.top - S.base >= S.stacksize) {//栈满，追加存储空间
        S.base = (ElemType *) realloc ( S.base,
            (S.stacksize + STACKINCREMENT) *sizeof (ElemType));
       if (!S.base) exit (OVERFLOW); //存储分配失败
       S.top = S.base + S.stacksize;
       S.stacksize += STACKINCREMENT;
   }
   *S.top++ = e;   //  这一行等价于 *S.top=e; S.top++;
    return OK;
}

顺序栈的出栈(Pop):

Status Pop (SqStack &S, SElemType &e) {
     // 若栈不空，则删除S的栈顶元素，
     // 用e返回其值，并返回OK；
     // 否则返回ERROR
    if (S.top == S.base) return ERROR;
    e = *--S.top; // 等价于 --S.top; e = *S.top;
    return OK;
}

链栈的表示和实现

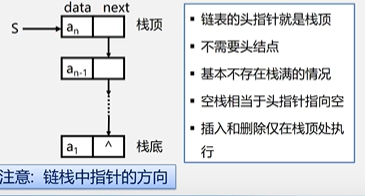
链栈的表示：
链栈是运算受限的单链表，只能在链表头部进行操作
链栈的定义

typedef struct SNode {
   SElemType    data;
   struct SNode  *next;
} SNode ,*LinkStack; 

LinkStack  S;  //声明栈

链栈的存储结构

栈顶指针就是链表的头指针

链栈的初始化

void InitStack(LinkStack &S){
 //构造一个空栈，栈顶指针置为空
  S= NULL;
  return OK;
  }

链栈的入栈(Push)

Status Push(LinkStack &S , SElemType e){  	p=(LinkStack)malloc(sizeof(SNode));    //生成新结点p  	
if (!p) exit(OVERFLOW);  	
	p->data=e; 
	p->next=S;
	 S=p; 
     return OK; 
}

链栈的出栈(Pop)

Status Pop (LinkStack &S,SElemType &e){
	if (S==NULL) return ERROR;
 	e = S-> data;  p = S;   S =  S-> next;
 	free(p);   
	return OK;
  } 

队列

队列的定义和特点

队列的定义：
队列是限定仅在表尾进行插入操作，仅在表头进行删除操作的线性表
队列的特点：
只能在对首和队尾运算，且访问结点是依照先进先出(FIFO)的原则。
逻辑结构
与同线性表相同，仍为一对一的关系
存储结构
顺序队或链队，以循环顺序队列更常见

抽象数据类型队列的定义

ADT Queue {
    数据对象：
               D＝{ai | ai∈ElemSet, i=1,2,...,n, n≥0}
    数据关系：
               R1＝{ <a i-1,ai > | ai-1, ai ∈D, i=2,...,n}
       约定其中a1 端为队列头， an 端为队列尾
    基本操作：。。。
} ADT Queue

队列的顺序表示和实现

#define MAXQSIZE  100  //最大队列长度
  typedef struct {
     QElemType  *base;  // 动态分配存储空间
     int  front;     // 头指针，若队列不空，指向队列头元素
     int  rear;      // 尾指针，若队列不空，指向队列尾元素的下一个位置
  } SqQueue;

假溢出
当front≠0,rear=M时再有元素入队发生溢出——假溢出

为了解决假溢出，我们引入循环队列

循环队列

入队列操作

    Q.base[Q.rear] = e; 
    Q.rear = (Q.rear+1) % maxsize;

出队列操作

    e = Q.base[Q.front];   
    Q.front = (Q.front+1) % maxsize;

循环队列中判断队满队空
在循环队列中 当front==rear时可能会出现队空和队满两种情况，所以在队列中判断队空，队满的方法在循环队列中并不适用。
解决方案：

通过少用一个元素空间来判断队空队满。
队空：front ==rear
队满：(rear+1)%M == front

循环队列的基本操作

1、初始化循环队列

Status InitQueue (SqQueue &Q) {
   // 构造一个空队列Q
   Q.base = (QElemType *) malloc 
           (MAXQSIZE *sizeof (QElemType));
    if (!Q.base) exit (OVERFLOW);            // 存储分配失败
    Q.front = Q.rear = 0;
    return OK;
 }```
**2、计算长度**

```c
int  QueueLength (SqQueue Q){
    return (Q.rear-Q.front+MAXQSIZE)%MAXQSIZE;                             
 }

入队列

Status EnQueue (SqQueue &Q, QElemType e) {      // 插入元素e为Q的新的队尾元素
    if ((Q.rear+1) % MAXQSIZE == Q.front) 
        return ERROR; //队列满
    Q.base[Q.rear] = e;
    Q.rear = (Q.rear+1) % MAXQSIZE;
    return OK;
}

出队列

Status DeQueue (LinkQueue &Q,QElemType &e){
   if(Q.front==Q.rear) return ERROR;
   e=Q.base[Q.front];
   Q.front=(Q.front+1)%MAXQSIZE;
   return OK;
}

链队列

链队列的类型定义

typedef struct {       // 链队列类型
    QueuePtr  front;  // 队头指针
    QueuePtr  rear;   // 队尾指针
} LinkQueue;

typedef struct QNode {       // 结点类型
    QElemType      data;
    struct QNode  *next;
  } QNode, *QueuePtr;

链队列的基本操作

1、链队列初始化

Status InitQueue (LinkQueue &Q) {
   // 构造一个空队列Q
   Q.front = Q.rear =
               (QueuePtr)malloc(sizeof(QNode));
   if (!Q.front) exit (OVERFLOW);             //存储分配失败
   Q.front->next = NULL;
   return OK;
}

2、入队列(采用尾插法)

Status EnQueue (LinkQueue &Q, QElemType e) {
    // 插入元素e为Q的新的队尾元素
    p = (QueuePtr) malloc (sizeof (QNode));
    if (!p)  exit (OVERFLOW);   //存储分配失败
    p->data = e;   p->next = NULL;
    Q.rear->next = p;    
    Q.rear = p;
    return OK;
}

3、链队列出队

Status DeQueue (LinkQueue &Q, QElemType &e) {
  // 若队列不空，则删除Q的队头元素，
  //用 e 返回其值，并返回OK；否则返回ERROR
   if (Q.front == Q.rear)    return ERROR;
   p = Q.front->next;   e = p->data;
   Q.front->next = p->next;
   if (Q.rear == p)  Q.rear = Q.front;
   free (p);      return OK;
}

4、求链队列的对头元素

Status GetHead (LinkQueue Q, QElemType &e){
   if(Q.front==Q.rear) return ERROR;
   e=Q.front->next->data;
   return OK;
}

5、销毁链队列

Status DestroyQueue(LinkQuene &Q){
 while(Q.front){
 	p = Q.front->next;
 	free(Q.front);
 	Q.front = p;}
 	return OK;
 	}