作者：RayChiu_Labloy
版权声明：著作权归作者所有，商业转载请联系作者获得授权，非商业转载请注明出处

---

目录

单高斯分布GM估计参数

关于高斯分布 

高尔顿钉板 

单维高斯概率密度函数

单维高斯GM参数估计过程

首先定义似然函数

让ℓ(λ)对u求偏导数，然后令其等于0，可以得到 

让ℓ(λ)对σ求偏导数，然后令其等于0，可以得到  

混合高斯分布GMM的参数估计

什么是GMM?

举个栗子

GMM的似然函数

公式 

怎么估计数据来源于哪个分布?

针对似然函数尝试用极大似然估计的方法来解GMM模型

EM算法求解GMM

E步：

M步：

---

单高斯分布GM估计参数

关于高斯分布 

高尔顿钉板 

        自然界中，很多事物的取值服从高斯分布。如高尔顿钉板：

        每次弹珠往下走的时候，碰到钉子会随机往左还是往右走，可以观测到多次随机过程结合的结果趋近于正太分布。

单维高斯概率密度函数

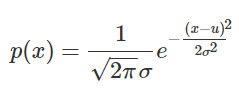
        其中表示均值，表示方差。

单维高斯GM参数估计过程

        我们的方法是根据极大似然估计求解高斯分布中的参数 λ = (,)。这里以一维高斯分布为例。

首先定义似然函数

 

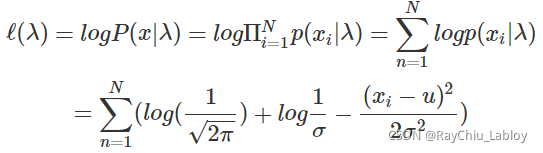
让ℓ(λ)对u求偏导数，然后令其等于0，可以得到 

 

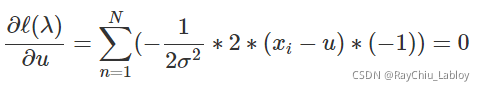
        可以得到的值为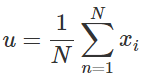，这不就是均值了么。

让ℓ(λ)对σ求偏导数，然后令其等于0，可以得到  

可以得到的值为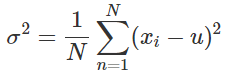，这不就是方差了么。

混合高斯分布GMM的参数估计

什么是GMM?

        GMM全称Gaussian Mixture  Model，是一种机器学习算法，是一种聚类模型，它是多个高斯分布函数的线性组合。

        理论上GMM可以拟合出任意类型的分布，通常用于解决同一集合下的数据包含多个不同的分布的情况（或者是同一类分布但参数不一样，或者是不同类型的分布，比如正态分布和伯努利分布）。

举个栗子

        如果二维空间有一些样本，如果没有GMM，用一个高斯分布来描述的情况：

         但是我们明显感觉样本是可以分为两个部分表示的，这时候GMM可以帮我们用两个高斯分布来表示：

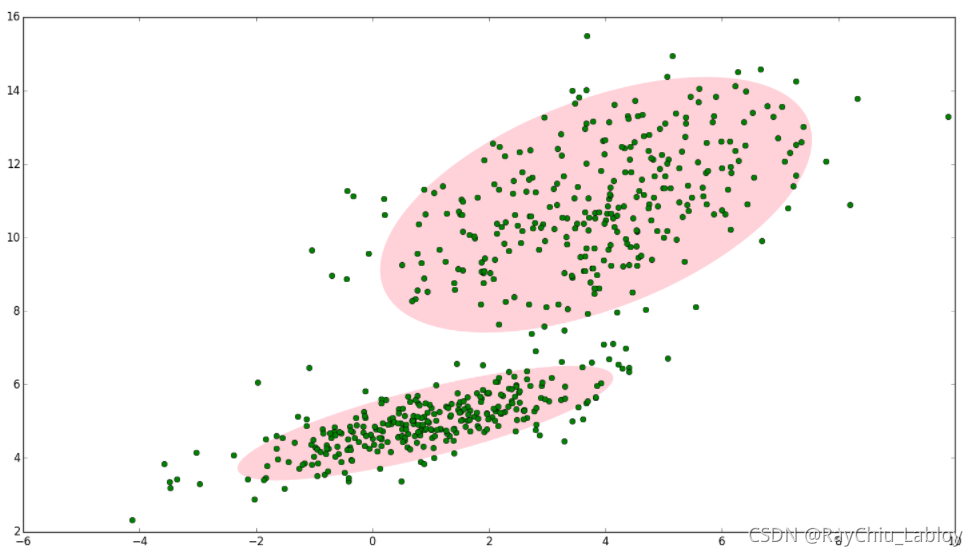
        两个高斯分布分别记为和，其中为均值，为协方差矩阵，显然这种方式更加合理，而这就是GMM模型了。

        那多维的高斯分布参数估计怎么来做？我们怎么求出所有的 μ，σ ？

GMM的似然函数

公式 

 

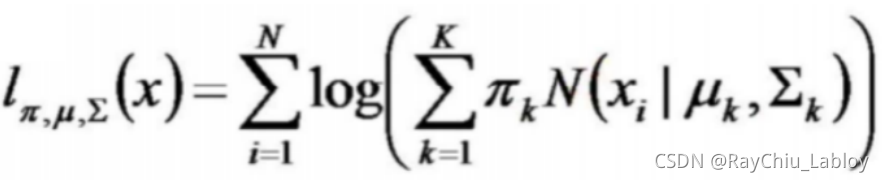
        N(x∣μk​,Σk​)称为混合模型中的第k个分量（component），是正太分布的概率密度函数。如前面图中样本的例子，有两个聚类，可以用两个二维高斯分布来表示，那么分量数K = 2。

         是混合系数（mixture coefficient），且满足：

 

 

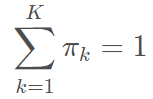
       可以理解这两个条件就是现验条件， 实际上，可以认为就是每个分量N(x∣μk​,Σk​)的权重。

       Σk=σk 是第k个分量协方差矩阵，μk是第k个分量均值。

         就是k个高斯所有情况都考虑进去的MLE极大似然估计的对数似然形式函数。

怎么估计数据来源于哪个分布?

        后验概率起着一个重要的作用，它也被称为响应度(responsibilities)，表示对于每个样本xi，它由第k个组份生成的概率，根据贝叶斯定理，后验概率可以表示为：

 

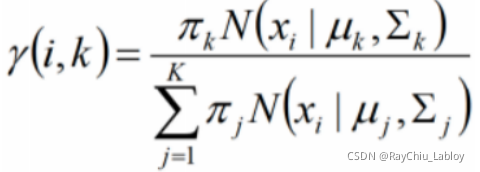
        这个式子是贝叶斯公式推导来的，Zk是某个类别： 

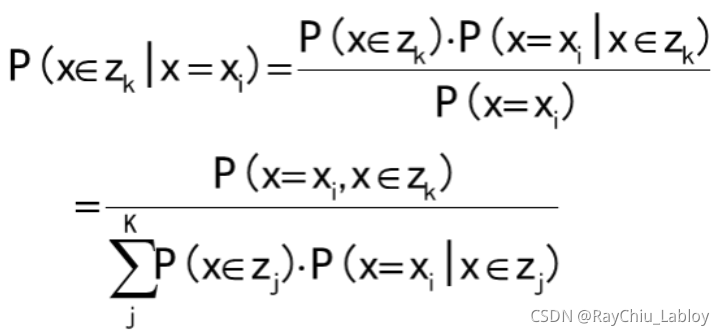
         所以，混合高斯模型并不是什么新奇的东西，它的本质就是融合几个单高斯模型，来使得模型更加复杂，从而产生更复杂的样本。理论上，如果某个混合高斯模型融合的高斯模型个数足够多，它们之间的权重设定得足够合理，这个混合模型可以拟合任意分布的样本。

针对似然函数尝试用极大似然估计的方法来解GMM模型

        高斯混合分布的形式由参数π,μ,Σ控制。解GMM模型，实际上就是求得这组参数，使得其确定的GMM模型最有可能产生采样的样本。看上去和单维高斯的问题类似，我们我可以尝试利用极大似然估计的方法来求解参数。

        步骤思路是先求导，然后令导数为0，得到模型参数π,μ,Σ，好像这样就解决了，然而仔细观察似然函数可以发现，对数似然函数里面，对数里面还有求和。实际上没有办法通过求导的方法来求这个对数似然函数的最大值，因此此时就用到EM算法求解了。

        单维高斯的情况是，如果我们已经清楚了某个变量服从的高斯分布，而且通过采样得到了这个变量的样本数据，想求高斯分布的参数μ,Σ，这时候极大似然估计可以胜任这个任务；而如果我们要求解的是一个混合模型，只知道混合模型中各个类的分布模型（譬如都是高斯分布）和对应的采样数据，而不知道这些采样数据分别来源于哪一类（隐变量），那这时候就可以借鉴EM算法。EM算法可以用于解决数据缺失的参数估计问题（隐变量的存在实际上就是数据缺失问题，缺失了各个样本来源于哪一类的记录）。

EM算法求解GMM

E步：

按照一般EM公式得到：

 

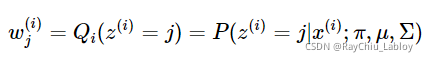
         这不就是在描述混合高斯分布时说到的很重要的后验概率么，表示样本xi由第j个组份生成的概率，Σ就是σ。

M步：

        求得Qi后之后，我们就得到了最贴近原对数似然函数的下界函数，那我们对它求极值就可以得到更新后的参数，先看一下这个下界函数：

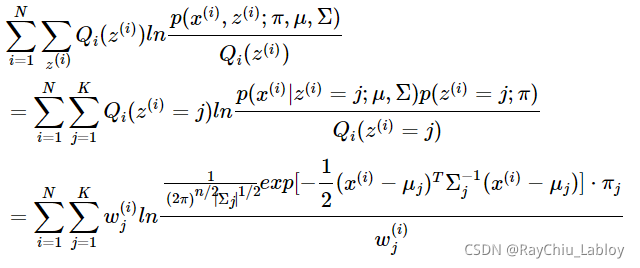
         这是将的k种情况展开后的样子，未知参数，，。

         固定 ， 对求导得：

 

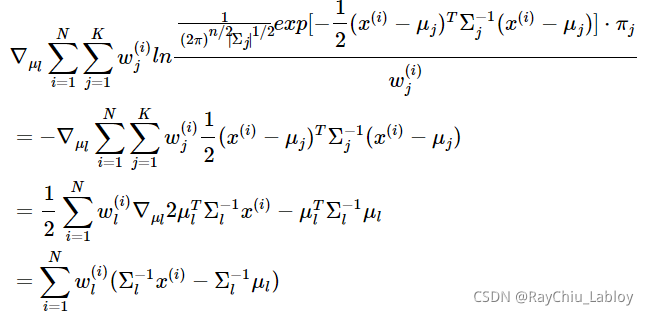
         令上式等于0，得到

 

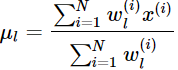
         这就是我们之前模型中的μ的更新公式。

        同样地，我们可以求出Σ的更新公式：

 

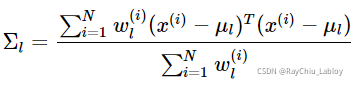
         对于π的求解可能复杂一些，首先我们把下界函数中与π不相关的项全部去掉，实际上需要优化的公式是：

 

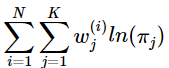
         根据，构造拉格朗日乘子：

 

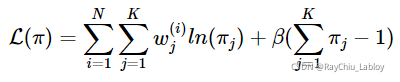
         还有会自动满足，求导得：

 

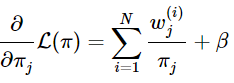
         令其等于0：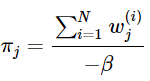

         这样就神奇地得到了β。

        于是得到M步中ππ的更新公式：

 

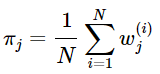
        我们再来看看这些参数的意义，其实未尝不符合我们的直觉认识。可以看做第 i 个样本属于第j类的概率，那么所有样本中属于第j类的个数就是之和，每个样本xi对应第j类的值就是，这样算的平均数就是第j类对应的μ，继续按照这个思路计算的方差就是第j类的Σ，第j类的概率就是第j类的个数除以总样本数。所以，GMM模型虽然推导起来有点吓人，但仔细想想它最后的结果也是符合我们的直觉认识的，每个样本都是一部分属于某一类，所有样本中的某一类的部分构成了这一类的分布。

参考：机器学习笔记-EM算法与混合高斯模型(GMM) - WarningMessage - 博客园

【机器学习系列】GMM第二讲：高斯混合模型Learning问题，最大似然估计 or EM算法？ - 知乎

高斯混合模型（GMM）及其EM算法的理解_小平子的专栏-CSDN博客_gmm

EM算法和GMM算法的相关推导及原理 - Baby-Lily - 博客园

如何理解GMM模型及应用-python黑洞网

梯度下降和EM算法：系出同源，一脉相承 - 科学空间|Scientific Spaces

【机器学习系列】GMM第二讲：高斯混合模型Learning问题，最大似然估计 or EM算法？_【AI机器学习与知识图谱】的博客-CSDN博客

【如果对您有帮助，交个朋友给个一键三连吧，您的肯定是我博客高质量维护的动力！！！】