决胜机房奥林匹克之LCA篇

前置知识：

二叉树

LCA：

https://www.luogu.com.cn/problem/P3379

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

LCA（Least Common Ancestors），即最近公共祖先，是指在有根树
中，找出某两个结点u和v最近的公共祖先。 ———来自百度百科

比方说样例：

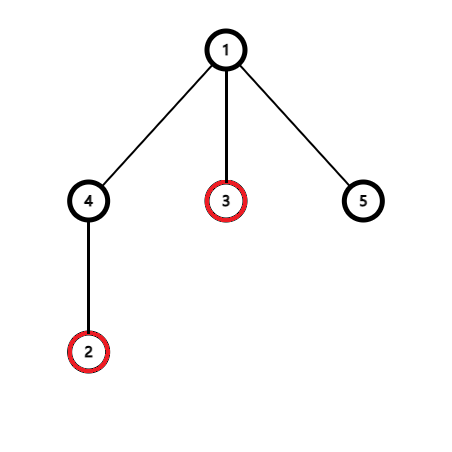
要你求3号点和2号点的lca。
显然，答案唯一，为根节点。

所以，lca有为一解，且必定有解。

那么，我们改如何去求解LCA呢？

暴力算法

考虑记录一下当前节点的深度。先让较深的那个节点跳到和另一个节点相同的深度（高度），再让两个节点一步一步地跳上去，直到跳到同意高度。
code：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 500005;
#define int long long
vector <int> p[maxn];
int f[maxn], dep[maxn];//dep记录深度，f[i]记录第i个点的父亲 

void dfs(int x, int father){
//	cout<<x<<' ';
	f[x] = father;
	dep[x] = dep[f[x]] + 1;
	int l = p[x].size();
	for(int i = 0; i < l; i++){
		if(p[x][i] != father)	dfs(p[x][i], x);//这里是为了防止重复遍历一个点 
	}
	return ;
} 

int lca(int x, int y){
	if(dep[x] < dep[y])	swap(x, y);//如果x的深度浅与y，则交换两数 
	while(dep[x] > dep[y]){
		x = f[x];//让较深的那个节点跳到和另一个节点相同的深度（高度） 
	}
	if(x == y){
		return x;//注意这里如果已经求出答案了就直接return 
	}
	while(x != y){
		x = f[x], y = f[y];//两个点一起爬 
	}
	return x;
}

signed main(){
	int n, m, s;
	cin>>n>>m>>s;
	for(int i = 1; i < n; i++){
		int x, y;
		cin>>x>>y;
		p[x].push_back(y);
		p[y].push_back(x);
	}
	dfs(s, s); //注意根节点的父亲是它本身 
	for(int i = 1; i <= m; i++){
		int x, y;
		cin>>x>>y;
		cout<<lca(x, y)<<endl;
	}
	return 0;
} 

这玩意预处理$O(n)$，每次查询$O(n)$,所以复杂度应该是$O(nm)$吧？

倍增优化

先鸽着