树是一种重要的数据结构。
许多事物存在层次关系。
分层次组织在管理上具有更高的效率。

文章目录

引子：查找
- 顺序查找
- 二分查找
树的定义
二叉树定义及性质
二叉树的存储结构
深度与高度
二叉树的操作集
- 创建
- 是否为空
- 遍历
- - 递归遍历
  - 非递归遍历
  - 层序遍历
- 遍历应用例子

引子：查找

对数据管理经常涉及到三个典型的操作：插入，删除，查找
如果对我们的一些事物或者数据采用层次的管理方法，效率是不是能得到提高呢？先分析一个基本的操作：查找

根据某个给定关键字 K，从集合 R 中找出关键字与 K 相同的记录。
静态查找：集合中记录是固定的
动态查找：集合中记录是动态变化的

一般的一种表示方法：把这个集合放到数组里，或者是在链表里。

一般的查找方法：顺序查找

顺序查找

#define MAXSIZE 10
typedef struct node{
	int element[MAXSIZE];
	int len;
}* List;
// 在索引 1~len 里存储 

int find(List L,int target){
	int i;
	L->element[0]=target;	// 建立哨兵 (在边界上设一个值,不需要每次去判断下标是不是达到了边界(i>0))
	for(i=L->len;L->element[i]!=target;i--);
	// 只有等于 target 的时候会退出
	return i;
}

对比不放哨兵的写法:
int find(List L,int target){
	int i;
	for(i=L->len;i>0&&L->element[i]!=target;i--);
	return i;	// 没找到就返回 0 
}

顺序查找：时间复杂度 O(n)

二分查找

通过进行事先的排序，时间复杂度 O(logn)
数据有序化之后，使得查找的过程就事先知道了它的顺序，这个顺序形成了一种树的结构
二分查找判定树
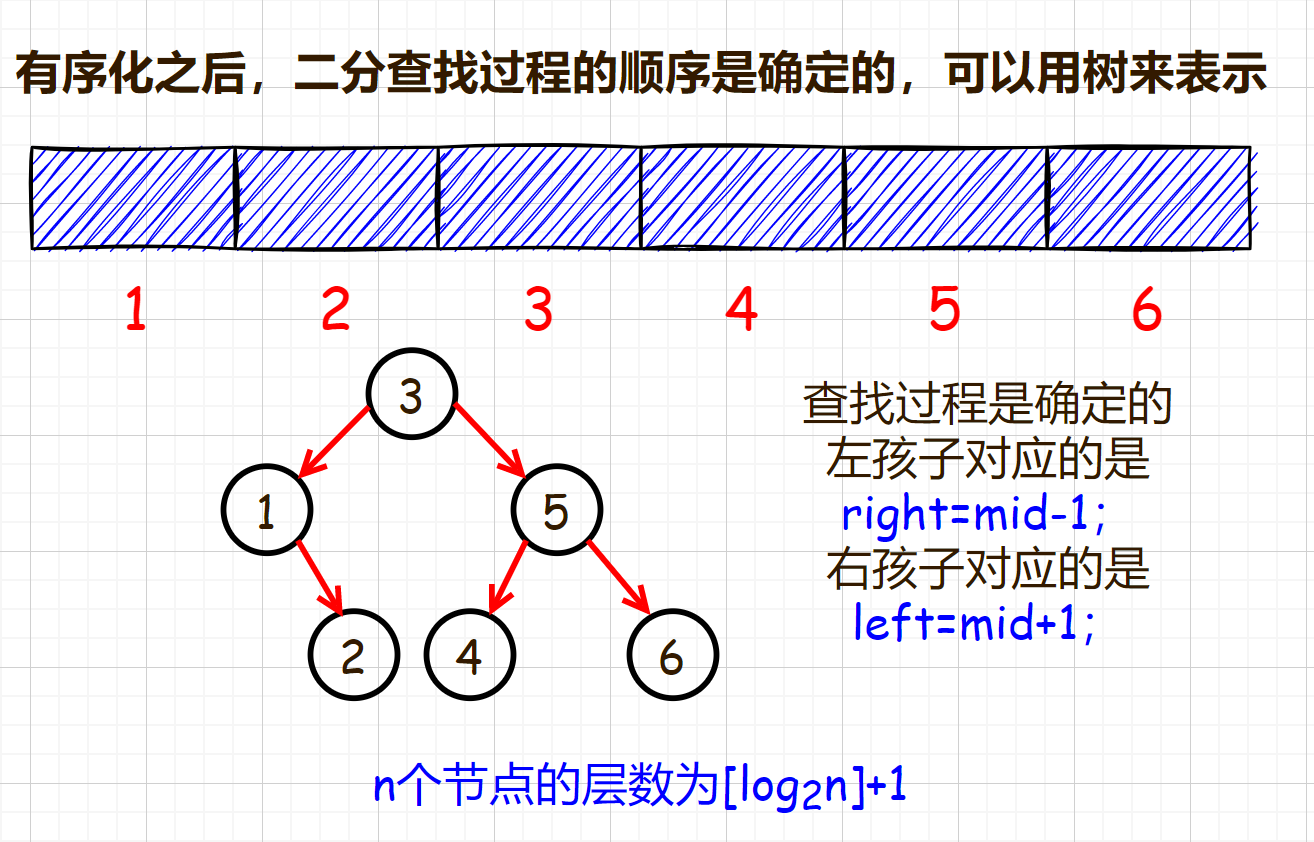
在这里插入图片描述
能不能把数据不一定放在数组里面，就按这样的一个层次化的结构来存储数据，是不是也会达到二分查找一样的效果？
以树的形式来存储我们的数据，使得我们的一些查找过程更加方便 →查找树（查找 logn，插入删除比在数组里方便得多，可以很好地解决动态查找问题）

树的定义

n个节点 (n>=0) 构成的有限集合
n=0时，空树
对任意一颗非空树(n>0)，由根及它的子树构成，子树之间彼此互不相交。
节点的度: 节点的子树个数
叶节点：度为0的节点
一颗 N 个节点的树有 N -1 条边。
一般的树都可以用 左儿子-右兄弟 表示

typedef struct Tndoe{
	ElementType data;
	struct Tnode *left;
	struct Tnode *right;
}*tree;
 // 二叉树的组织形式

搞清楚二叉树，也就解决了一般树的许多问题。

二叉树定义及性质

一个有穷的节点集合，可以为空。
不为空，则是由根节点和不相交的左子树，右子树构成。
二叉树的子树有左右顺序之分。
五种基本形态：
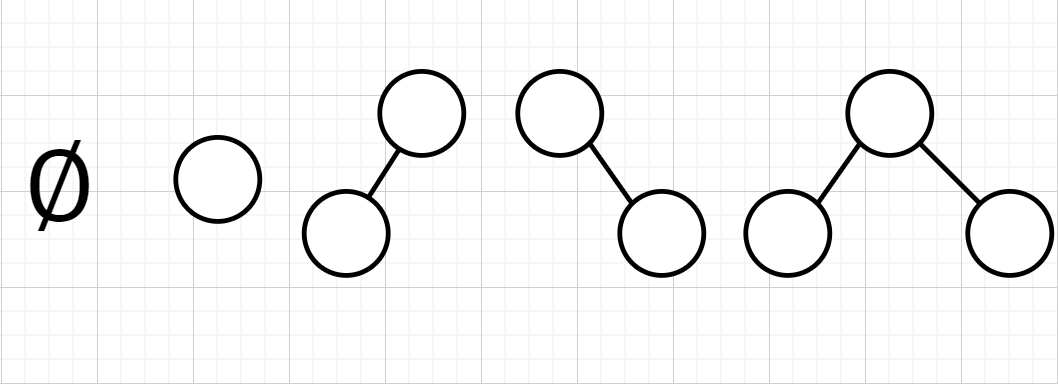
在这里插入图片描述
一些性质：
第 i 层的最大节点数为：2^i-1，i>=1
深度为 k 的二叉树有最大节点总数：2^k-1，k>=1（根节点深度为 1时）
度为2的节点个数+1=叶节点个数

二叉树的存储结构

二叉树如何进行表示？
1.顺序存储（数组）
适用于完全二叉树，从上到下，从左至右，依次顺序存储
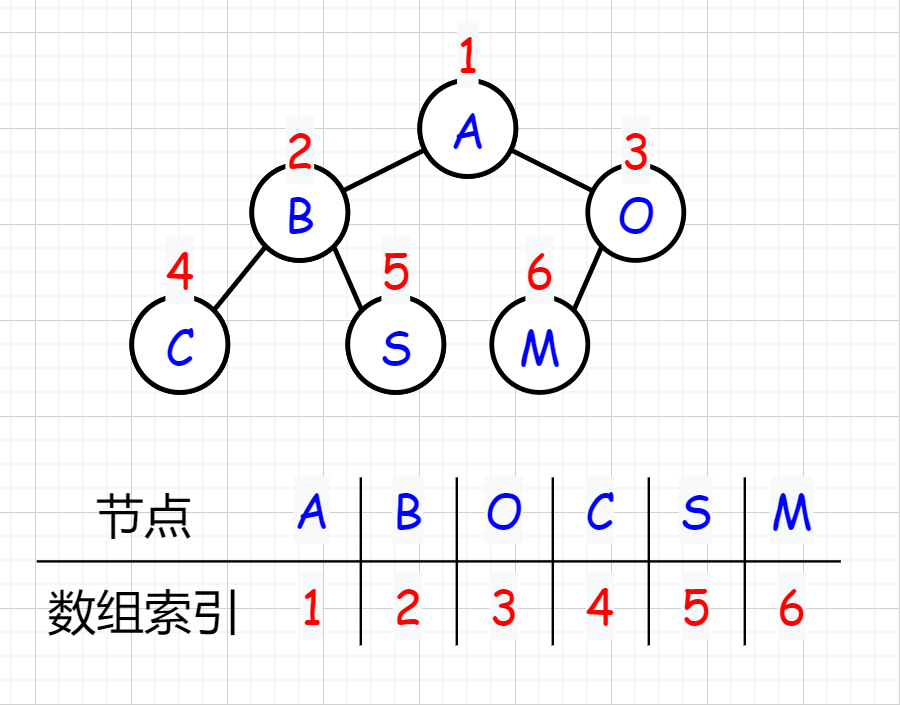
在这里插入图片描述
对 n 个节点的完全二叉树：
非根节点(序号 i >1)的父节点的序号是 [ i/2 ]
序号为 i 的节点的左孩子节点的序号是： 2i
序号为 i 的节点的右孩子节点的序号是： 2i+1
( 2i > n，没有左孩子。2i+1 > n，没有右孩子。)

对一般的二叉树，也可以用这种方式存储，但要补充成一个完全二叉树，缺的节点在数组的对应位置处留下空位
节点之间的对应关系依然存在，但这样存储就会造成一些空间浪费。

2.链式存储

typedef struct Tnode{
	ElementType data;
	struct Tnode *left;
	struct Tnode *right;
}*tree;

深度与高度

由根通往每个节点的路径是唯一的。
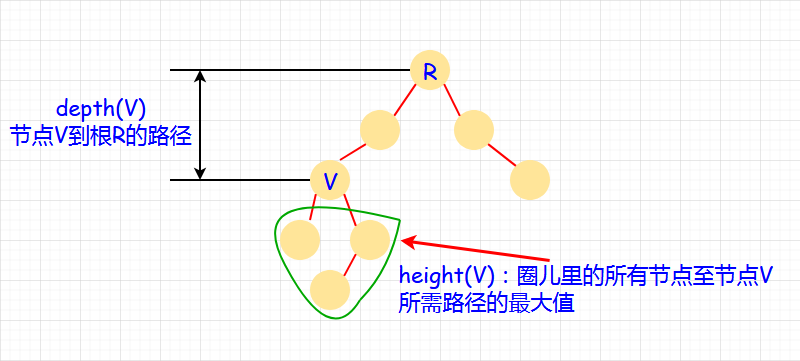
在这里插入图片描述

根节点 R 的深度是 0。
根节点 R 的高度=树的高度=树中所有节点深度的最大值。
叶节点的高度是 0。

二叉树的操作集

创建

typedef struct tree{
	char data;
	struct tree *left;
	struct tree *right;
}*Tree;
// 先序 创建
Tree Create_binary_tree(){
	char shu_ju;
	cin>>shu_ju;
	Tree  L;
	if(shu_ju=='#'){		// 没有 右儿子 或者 左儿子
		return NULL;
	}else{
		L=new struct tree;
		L->data=shu_ju;
		L->left=Create_binary_tree();
		L->right=Create_binary_tree();
		return L;
	}
}

是否为空

遍历

递归遍历

先序：根，左，右

// 先序 
void Pre_order(tree L){
	if(L){
		printf("%d",L->data);
		Pre_order(L->left);
		Pre_order(L->right);
	}
}

中序：左，根，右

// 中序 
void mid_order(tree L){
	if(L){
		mid_order(L->left);
		printf("%d",L->data);
		mid_order(L->right);
	}
}

后序：左，右，根

// 后序 
void post_order(tree L){
	if(L){
		post_order(L->left);
		post_order(L->right);
		printf("%d",L->data);
	}
}

先序，中序，后序遍历过程，经过节点的路线都是一样的，只是访问（print）各节点的时机不同。
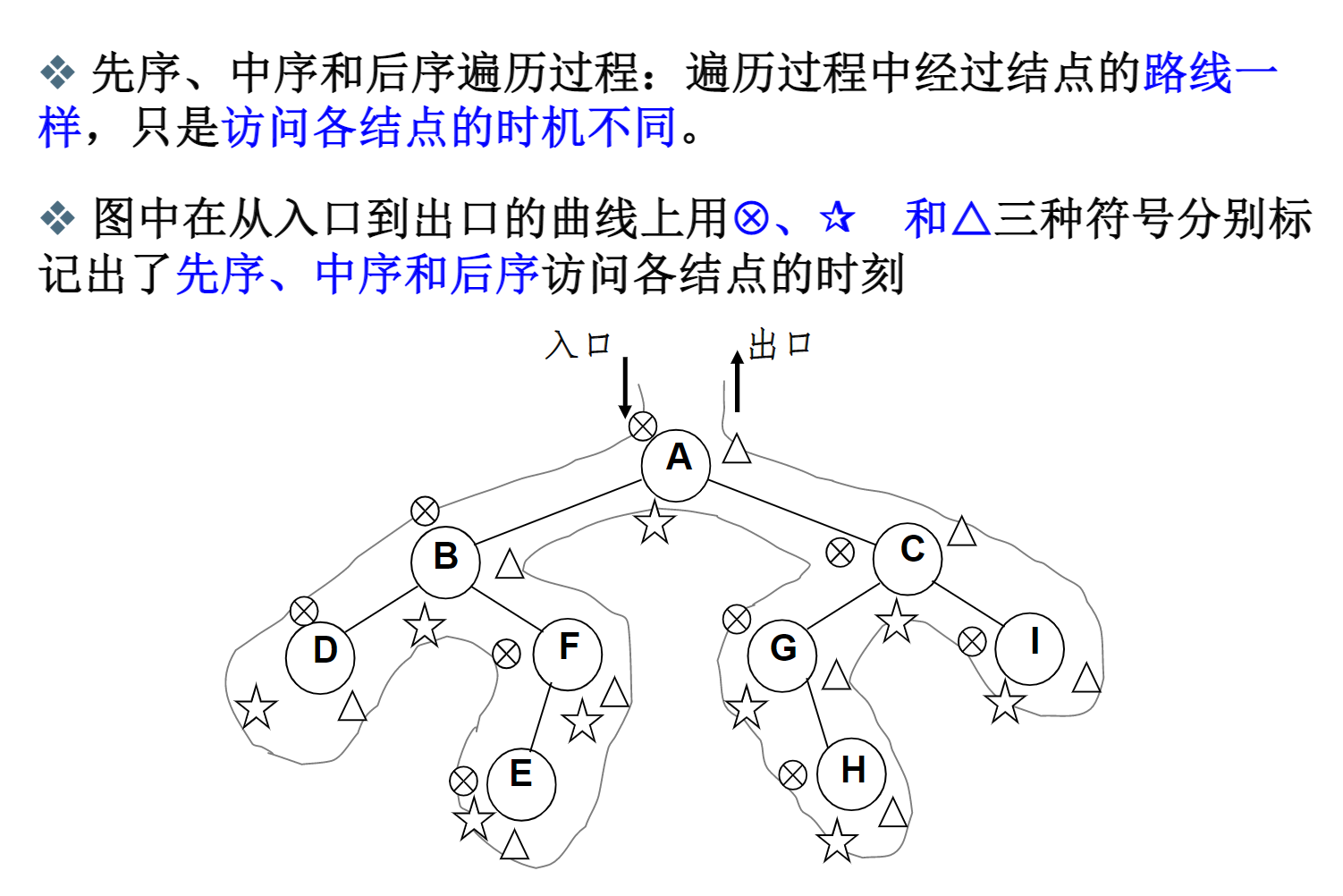
在这里插入图片描述

非递归遍历

中序非递归遍历：

void mid_order(tree L){
	tree p=L;
	Stcak s=CreatStack(MaxSize);			// 创建一个栈结构 
	while(p||!isempty(s)){			// 有一个不为空就继续循环 
		while(p){	 
			push(s,p);
			p=p->left;	// 一直向左并将沿途节点压入栈, 直到 节点 p 为空节点
		}
		if(!isempty(s)){
			p=pop(s);	// 往回走, 抛出一个元素
			printf("%d",p->data);
			p=p->right; // 转向 右子树, 如果没有右儿子(p==NULL), 就往回走, 再抛出一个元素
		}
	}
}

先序非递归遍历：

void Pre_order(tree L){
	tree p=L;
	Stack s=CreateStack(MaxSize);
	while(p||!IsEmpty(s)){
		while(p){
			push(s,p);
			printf("%5d",p->data);			// 一直向左 ,直到为空, 碰到即输出
			p=p->left;
		}
		if(!IsEmpty(s)){
			p=pop(s);		// 回头走
			p=p->right;				// 转向右子树, 如果没有  就再回头 走一步(pop), 看他的右子树 
		}
	}
}

后序非递归遍历：

// 借鉴了 先序  的非递归 , 先得到 一个 根右左 序列, 再逆序输出
void Post_order(tree L){
	tree p=L;
	Stack s=CreateStack(MaxSize);
	Stack result=CreateStack(MaxSize);	// result 用来放   根右左 次序
	while(p||!IsEmpty(s)){
		while(p){
			push(s,p);
			push(result,p);			// 碰到 即 存起来 
			p=p->right;
		}
		if(!IsEmpty(s)){
			p=pop(s);
			p=p->left;
		}
	}
	
	// 输出 数据		根右左 --> 左右根 
	while(!IsEmpty(result)){
		p=pop(result);
		printf("%5d",p->data);
	} 
}

层序遍历

利用队列
遍历从根节点开始，首先将根节点入队，然后执行循环；
（节点出队，左右儿子入队）直到队列里没有元素。

void layer_order(tree L){
	Queue Q;tree T;
	if(!L)return;	 
	Q=CreatQueue(MaxSize);		// 创建队列结构 
	AddQ(Q,L);
	while(!isempty(Q)){
		T=DeleteQ(Q);	//  出队 
		printf("%d",T->data);
		if(T->left)AddQ(Q,T->left);		// 将其 左右儿子  进队 
		if(T->right)AddQ(Q,T->right); 
	} 
}

将层序遍历中的队列改为堆栈，也是一种遍历方式- - -> 根右左

遍历应用例子

利用二叉树遍历这样的一种程序框架或者是思想，可以做一些二叉树应用的一些问题

输出叶子结点：

在进行遍历输出时，只需加上一层判断（左右儿子是否都没有），就可以了。

求二叉树高度：
求一个树的高度，必须要知道其左右两个子树的高度，所以应该用后序遍历

int Get_Height(Bintree B){
	int hl,hr,height;
	if(B){
		hl=Get_Height(B->left);
		hr=Get_Height(B->right);
		height=hl>=hr?hl:hr;
		return height+1;
	}else{
		return 0;							// 空树 高度 为 0; 
	}
}

由两种遍历序列确定二叉树，必须有一个是中序序列

树 / 二叉树的基本内容