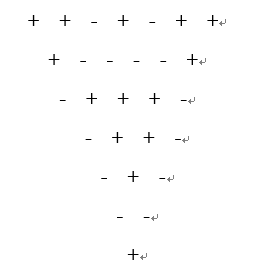文章目录
- 回溯法
- 1.概述
- 2.三个概念
- 3.解题步骤
- 一:符号三角形问题
- 1.问题描述
- 2.解题思路
- 3.程序代码
- 二:整数变换问题
- 1.问题描述
- 2.程序代码
- 三:子集和问题
- 1.问题描述
- 2.程序代码
- 四:工作分配问题
- 1.问题描述
- 2.程序代码
回溯法
1.概述
回溯(backtracking)法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
回溯法是一个既带有系统性又带有跳跃性的的搜索算法。它在包含问题的所有解的解空间树中,按照深度优先的策略,从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时,总是先判断该结点是否肯定不包含问题的解。如果肯定不包含,则跳过对以该结点为根的子树的系统搜索,逐层向其祖先结点回溯。否则,进入该子树,继续按深度优先的策略进行搜索。回溯法在用来求问题的所有解时,要回溯到根,且根结点的所有子树都已被搜索遍才结束。而回溯法在用来求问题的任一解时,只要搜索到问题的一个解就可以结束。这种以深度优先的方式系统地搜索问题的解的算法称为回溯法,它适用于解一些组合数较大的问题.
适用条件
问题的解用向量表示 X = (x1, x2, …, xn)
需要搜索一个或一组解 满足约束条件的最优解
2.三个概念
**约束函数:**约束函数是根据题意定出的。通过描述合法解的一般特征用于去除不合法的解,从而避免继续搜索出这个不合法解的剩余部分。因此,约束函数是对于任何状态空间树上的节点都有效、等价的。
**状态空间树:**一个问题的解可以表示成解向量X = (x1, x2, …, xn),X中每个分量xi所有取值的组合构成问题的解向量空间,简称解空间或者解空间树,又称为状态空间树,是一个对所有解的图形描述。树上的每个子节点的解都只有一个部分与父节点不同。
**扩展节点、活结点、死结点:**所谓扩展节点,就是当前正在求出它的子节点的节点,在DFS中,只允许有一个扩展节点。活结点就是通过与约束函数的对照,节点本身和其父节点均满足约束函数要求的节点;死结点反之。由此很容易知道死结点是不必求出其子节点的(没有意义)。
由于采用回溯法求解时存在退回到祖先结点的过程,所以需要保存搜索过的结点。通常采用: 定义栈来保存 采用递归方法
用回溯法通常采用两种策略(均称为剪枝函数)避免无效搜索。 用约束函数在扩展结点处剪除不满足约束条件的路径
用限界函数剪去得不到问题的解或最优解的路径
3.解题步骤
(1)描述解的形式,定义一个解空间,它包含问题的所有解,这一步主要明确问题的解空间树。
(2)确定结点的扩展搜索规则。
(3)构造约束函数(用于杀死节点)。然后就要通过DFS思想完成回溯,DFS可以采用递归回溯或者非递归(迭代)回溯。 确定问题的解空间 -->
确定结点的扩展搜索规则–> 以DFS方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索。
一:符号三角形问题
1.问题描述
符号三角问题:下面都是“-”。 下图是由14个“+”和14个“-”组成的符号三角形。2个同号下面都是“+”,2个异号下面都是“-”。
在一般情况下,符号三角形的第一行有n个符号。符号三角形问题要求对于给定的n,计算有多少个不同的符号三角形,使其所含的“+”和“-”的个数相同。
参考代码如下,请在此基础上,实现如下功能:
- 分别输出n的值为1----20时,对应的符号三角形个数,如没有满足条件的符号三角形,则输出0
- 输入一个整数n,输出对应的符号三角形的个数,并依次显示出所有的符号三角形。
2.解题思路
(1)解题思路:
1、不断改变第一行的每个符号,搜索符合条件的解,可以使用递归回溯。
为了便于运算,设+ 为0,- 为1,这样可以使用异或运算符表示符号三角形的关系:
++为+即0^0=0, --为+即1^1=0, ±为-即0^1=1, -+为-即1^0=1
2、因为两种符号个数相同,可以对题解树剪枝
当所有符号总数为奇数时无解,当某种符号超过总数一半时无解
(2)算法设计
在符号三角形的第一行的前i个符号x[1:i]确定后,就确定了一个由i*(i+1)/2个符号组成的符号三角形。
下一步确定了x[1:i]的值后,只要在前面确定的符号三角形的右边加一条边,就可以扩展为x[1:i]所对应的符号三角形。
在回溯法搜索过程中可用当前符号三角形所包含的“+”号个数与“-”号个数均不超过n*(n-1)/4作为可行性约束,用于剪去不满足约束条件的子树。
3.程序代码
public class Triangles{
static int n, //第一行符号的个数
count, //n*(n+1)/2
half; //当前"+"的个数
static int [][] p; //符号三角形矩阵
static long sum; // 已找到的符号三角形数
public static long compute(int nn)
{
n=nn;
count=0;
sum=0;
half=n*(n+1)/2;
if (half%2==1) return 0;
half=half/2;
p=new int[n+1][n+1];
for(int i=0;i<=n;i++)
for(int j=0; j<=n;j++)
p[i][j]=0;
backtrack(1);
return sum;
}
public static void backtrack (int t)
{
if((count>half)||(t*(t-1)/2-count>half))
{
return; //剪去不满足约束的子树
}
if(t>n)
{
sum++; //找到一个满足要求的三角形
/*
可在此处加入代码,输出当前解对应的符号三角形
*/
}
else
for(int i=0;i<2;i++)
{//子树
p[1][t]=i;
count+=i;
for(int j=2;j<=t;j++) //该子树形成的三角形
{
p[j][t-j+1]=p[j-1][t-j+1]^p[j-1][t-j+2];
count+=p[j][t-j+1];
}
backtrack(t+1);
for(int j=2;j<=t;j++) //回溯恢复
count-=p[j][t-j+1];
count-=i;
}
}
public static void main(String[] args) {
int n=4; long result;
result=compute(n);
System.out.println(String.format("result=%d",result));
}
}
package suanfa;
public class suanfa1 {
static int n;//第一行的符号个数
static int half;//n*(n+1)/4
static int count;//当前“+”或者“-”的个数
static int[][] p;//符号三角形矩阵
static long sum;//已找到的符号三角形的个数
public static float Compute(int nn) {
n = nn;
count = 0;
sum = 0;
half = (n*(n+1))>>1;
if((half>>1)<<1 != half) {
return 0;
}
half = half>>1;
p = new int[n+1][n+1];
backtrack(1);
return sum;
}
/**
* 算法1
* @param t
*/
public static void backtrack01(int t) {
if(count>half || (t*(t-1)/2-count > half)) {//对题解树的剪枝
return;
}
if(t>n) {
sum++;//符号三角形的总数目+1
}
else {
//每个位置都有两种情况0,1
for(int i = 0;i<2;i++) {
p[1][t] = i;
count += i;//对"-"个数进行技术,为了进行剪枝操作
//接下来绘制其余的n-1行
for(int j = 2;j<=t;j++) {
//通过异或的方式求其余行数的放置方式
p[j][t-j+1] = p[j-1][t-j+1]^p[j-1][t-j+2];
count += p[j][t-j+1];
}
backtrack01(t+1);
//恢复现场
for(int j = 2;j<=t;j++) {
count -= p[j][t-j+1];
}
count -= i;
}
}
}
public static void backtrack(int t) {
if((count>half)||((t*(t-1)/2-count > half)) ){//对题解树的剪枝
return;
}
if(t>n) {
sum++;
//打印符号三角形
for(int i =1;i<=n;i++) {
for(int k = 1;k<i;k++) {
System.out.print(" ");
}
for(int j =1;j<=n;j++) {
if(p[i][j] == 0 && j<=n-i+1) {
System.out.print("+" + " ");
}
else if(p[i][j] == 1 && j<=n-i+1) {
System.out.print("-" + " ");
}
else {
System.out.print(" ");
}
}
System.out.println();
}
System.out.println();
}
else {
//每个位置都有两种情况0,1
for(int i =0;i<2;i++) {
p[1][t] = i;
count += i;//计算“-”的个数
//接下来绘制其余的n-1行
for(int j = 2;j<=t;j++) {
//通过异或的方式求其余行数的放置方式
p[j][t-j+1] = p[j-1][t-j+1]^p[j-1][t-j+2];
count += p[j][t-j+1];
}
backtrack(t+1);
//恢复现场
for(int j =2;j<=t;j++) {
count -= p[j][t-j+1];
}
count -= i;
}
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
float SUM = Compute(4);
System.out.print("总数: " + SUM);
}
}
二:整数变换问题
1.问题描述
整数i的两种变换定义为 , (向下取整);设计一个算法求给定两个整数a和b,用最少次数的 和 变换将整数a变换为b;例如
实现提示:
观察f和g两个操作可知,f总是使得i变大,g总是使得i变小。因此在决定让x执行哪个操作之前可以先判断i和目标值m之间的大小关系。如果x>m,就让其执行g操作;反之,执行f操作。
问题的解分为两种情况,一种是有解,即n可以通过函数变换成m;另一种是无解,即n无法通过函数变换成m。
有解的情况比较容易,只需要判断最后的i是否等于m即可。如果i等于m,那么说明n已经被变换成m了,递归返回。
无解的情况可用下例分析。假设输入n=9,m=5。
n>m,执行g,n=[9/2]=4
n<m,执行f,n=34=12
n>m,执行g,n=[12/2]=6
n>m,执行f,n=[6/2]=3
n<m,执行g,n=33=9
n>m,执行f,n=[9/2]=4
如果n的值陷入了一个重复的循环,如果在递归的过程中,出现了前面计算过的元素,那就说明n是无法转换成m的。这种方法实现稍微复杂,需要判断当前所求出的数值之前是否出现过。 另一种简单的处理方式: 对于m无论如何变换都不能变为n的情况,可以加一个判断条件,比如深度达一个较大值为止(如1000)。
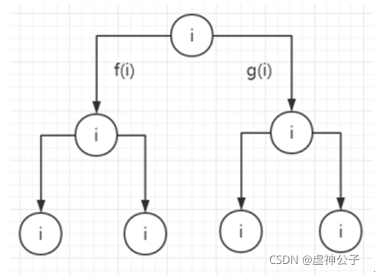
回溯法, 用子集树实现,子集树结构为:
回溯返回条件有两个,一个是i等于m,另一个是出现了重复的数字。第二个返回条件可以用一个函数test来判断。
剪枝条件:
显式约束:如果x>m,就剪掉它的左子树;如果x<m,就剪掉它的右子树;
隐式约束:如果在某次计算的过程中发现当前的计算次数已经大于或等于最少计算次数了,那么就剪掉这个分支。
2.程序代码
package suanfa;
import java.util.Scanner;
public class suanfa1 {
static int m,n1; //n1方便后面的输出形式
static int tempcount,bestcount;//当前变换次数,最佳变换次数
static int[] temp1=new int[100];
static int[] temp2=new int[1000];
public static void main(String args[]){
Scanner input=new Scanner(System.in);
System.out.println("请输入需变换的整数");
int n=input.nextInt();
n1=n;
System.out.println("请输入需变换后的整数");
m=input.nextInt();
tempcount=0;
bestcount=100;
test(n);
}
//实现方法
public static void test(int n){
if(tempcount>99){ //最好的变换次数已经大于某个特定的值,是无解情况(隐式约束)
System.out.println("无解");
}
else{
if(n==m){ //有解情况
if(tempcount<bestcount) //
bestcount=tempcount;
System.out.println("最佳变换次数:"+bestcount);
System.out.printf("%d=",m);
for(int i=bestcount;i>=1;i--){
if(temp2[i]==2)
System.out.print("f");
if(temp2[i]==1)
System.out.print("g");
}
System.out.printf("(%d)",n1);
}
else if(n>m){ //n>m走这个分支 ,起到剪枝作业
n=g(n);
tempcount++;
temp2[tempcount]=1;
test(n);
}
else { //n<m走这个分支
n=f(n);
tempcount++;
temp2[tempcount]=2;
test(n);
}
}
}
//f(i)=3*i
public static int f(int n){
n=3*n;
return n;
}
//g(i)=i/2
public static int g(int n){
n=n/2;
return n;
}
}
三:子集和问题
1.问题描述
给定集合S,S中有n个正整数,M是一个正整数。子集和问题判定是否存在S的一个子集S1,使得S1中各元素之和等于M。请设计回溯法求解子集和问题,如果问题无解,输出“No Solution”,问题有解,则输出满足子集S1中各元素的值。
2.程序代码
package suanfa;
import java.util.Scanner;
public class suanfa2 {
public static void main(String[] args) {
SubSet subSet=new SubSet();
Scanner scanner = new Scanner(System.in);
System.out.println("输入长度和所求子集总和");
int len,m;
len=scanner.nextInt();
m=scanner.nextInt();
int[] nums=new int[len];//初始数组
int[] sets=new int[len];//子集数组
System.out.println("输入初始数组");
for(int i=0;i<len;i++)
nums[i]=scanner.nextInt();
subSet.setNums(nums);
subSet.setSets(sets);
subSet.setTotal(m);
subSet.setCount(0);
subSet.setErrStr("No Solution");
subSet.backTrack(0);
if(subSet.getCount()==0){
System.out.println(subSet.getErrStr());
}
}
}
subSet.class
package suanfa;
import java.util.Arrays;
public class SubSet{
private int[] nums;//初始数组
private int[] sets;//子集数组
private int total;//和
private int count;//存在子集数
private String errStr;//没有子集的时候输入的语句
public void setErrStr(String errStr) {
this.errStr = errStr;
}
public void setNums(int[] nums) {
this.nums = nums;
}
public void setSets(int[] sets) {
this.sets = sets;
}
public void setTotal(int total) {
this.total = total;
}
public void setCount(int count) {
this.count = count;
}
public int[] getNums() {
return nums;
}
public int[] getSets() {
return sets;
}
public int getTotal() {
return total;
}
public int getCount() {
return count;
}
public String getErrStr() {
return errStr;
}
public void backTrack(int idx){
if(total==0){
System.out.println(Arrays.toString(sets));
count++;
return;
}
if(idx==nums.length||total<0)
return;
else{
for(int i=idx;i<nums.length;i++){
if(nums[i]<=total){
sets[i]=nums[i];
total-=nums[i];
backTrack(i+1);
sets[i]=0;
total+=nums[i];
}
}
}
}
}
测试数据1:
输入:
4 31
13 24 11 7
输出:
[13, 0, 11 , 7]
[0, 24, 0 , 7]
测试数据2:
输入:
5 235
123 55 9 4 11
输出:
No Solution
四:工作分配问题
1.问题描述
设有n件工作分配给n个人。将工作i分配给第j个人需要支付的劳务费为cij,请设计算法,为每个人都分配1件不同的工作,并使得总劳务费达到最小。
实现提示:该问题的解空间是一棵排列树,可用搜索排列树的回溯框架实现。
输入格式:
输入数据的第一行为1 个正整数n (1≤n≤20),表示工作的数量,随后输入n行,每行n个数,表示相应的劳务费。
输入样例:
3
10 2 3
2 3 4
3 4 5
输出样例:
9
2.程序代码
package suanfa;
import java.util.Scanner;
public class suanfa3 {
public static int sum = 0,n;
public static int [] [] num ;
public static boolean [] bool;
public static int min = Integer.MAX_VALUE;
public static void main(String[] args) {
Scanner sc =new Scanner(System.in);
n = sc.nextInt();
num = new int [n+1][n+1];
bool = new boolean [n+1];
for (int i = 1; i <=n; i++) {
for (int j = 1; j <=n; j++) {
num[i][j]=sc.nextInt();
}
}
f(1);
System.out.println(min);
}
public static void f(int a){
if(a==n+1){
if(sum<min){
min=sum;
}
return;
}
for (int i = 1; i <=n; i++) {
if(!bool[i]){
sum+=num[a][i];
bool[i]=true;
f(a+1);
sum-=num[a][i];
bool[i]=false;
}
}
}
}