1.
一个二维数组 按从小到大排列,我们可以按照 分块查询的方式 查找此元素,找到了 返回其下标
(1) 普通版
#include <stdio.h>
#include <stdlib.h>
int FindValue(int arr[][5], int abs, int ord, int val)
{
int i = 0;
while (val > arr[i][ord - 1] && i<abs-1) //寻找val所在的行
{
i++;
}
if (val == arr[i][ord - 1]) //恰好val==行末
{
return i*ord + ord-1;
}
int j = ord - 1;
while (j>=0 && arr[i][j]>val) //在所在行进行线性查找
{
j--;
}
if (val > arr[i][j]) //大于最后一行的末尾元素,说明不存在此数
{
return -1;
}
if (j < 0) //没找到
{
return -1;
}
else //找到了
{
return i*ord + j;
}
}
void Judge(int result, int ord)
{
if (result == -1)
{
printf("对不起,数组中没有这个数!\n");
}
else
{
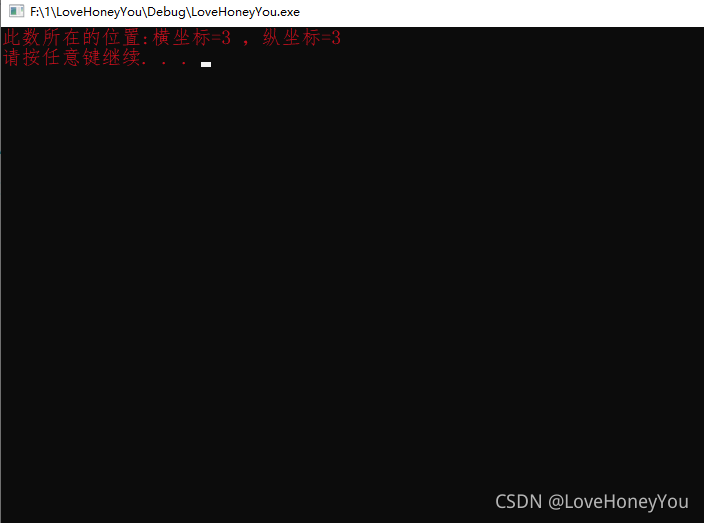
printf("此数所在的位置:横坐标=%d ,纵坐标=%d \n", result / ord + 1, result % ord + 1);
}
}
int main()
{
int arr[4][5] =
{
{ 1, 3, 5, 7, 9},
{11,13,15,17,19},
{21,23,25,27,29},
{31,33,35,37,39},
};
int val = 25;
Judge(FindValue(arr, 4, 5, val),5);
system("pause");
return 0;
} 
(2) 精简版
#include <stdio.h>
#include <stdlib.h>
int FindValue(int arr[][5], int abs, int ord, int val)
{
int i = 0;
while (val > arr[i][ord - 1] && i<abs)
{
i++;
}
if (i == abs)
{
return -1;
}
int j = ord - 1;
while (j >= 0 && arr[i][j]>val)
{
j--;
}
if (j >= 0 && arr[i][j] == val)
{
return i*ord + j;
}
else
{
return -1;
}
}
void Judge(int result, int ord)
{
if (result == -1)
{
printf("对不起,数组中没有这个数!\n");
}
else
{
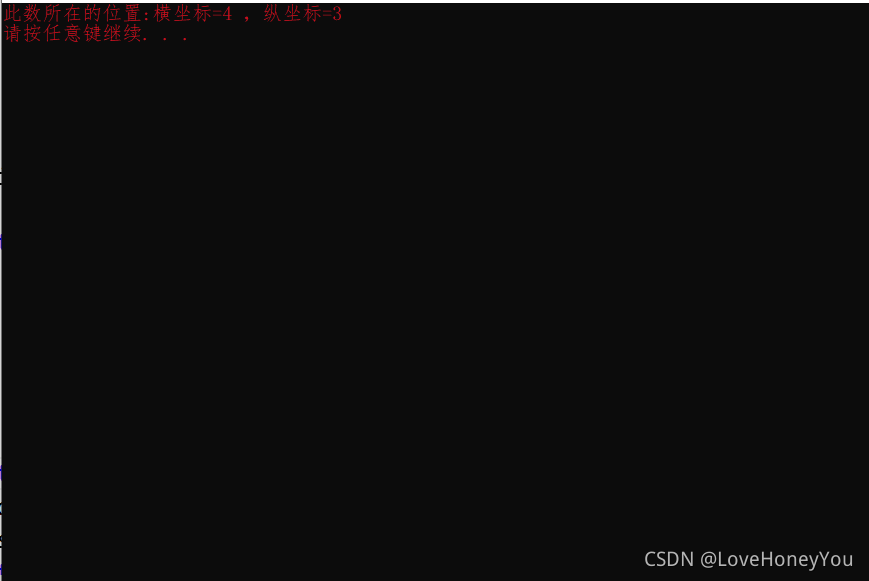
printf("此数所在的位置:横坐标=%d ,纵坐标=%d \n", result / ord + 1, result % ord + 1);
}
}
int main()
{
int arr[4][5] =
{
{ 1, 3, 5, 7, 9},
{11,13,15,17,19},
{21,23,25,27,29},
{31,33,35,37,39},
};
int val = 35;
Judge(FindValue(arr, 4, 5, val),5);
system("pause");
return 0;
}
有时候正向思维的确比逆向思维能简单不少~~~
2.
二分查询
#include <stdio.h>
#include <stdlib.h>
int Binary_Que(int *cp, int size,int val)
{
int left = 0;
int right = size - 1;
int pos = -1;
int mid = 0;
while (left <= right)
{
mid = (left + right) / 2;
if (cp[mid] == val)
{
pos = mid;
break; //返回下标
}
else if (cp[mid] < val)
{
left = mid + 1;
}
else
{
right = mid - 1;
}
}
return pos;
}
int main()
{
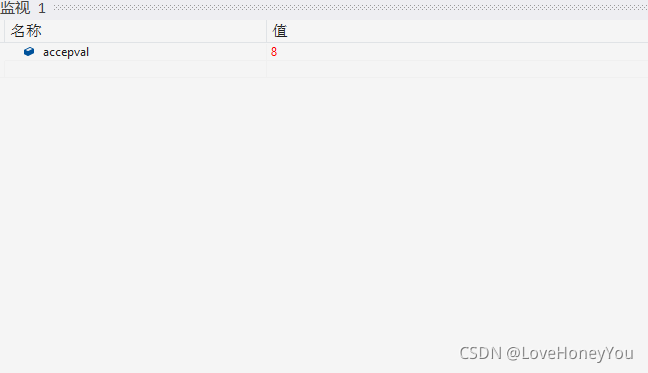
int arr[] = { 12, 23, 34, 45, 56, 78, 89, 90, 100, 110, 120 };
int size = sizeof(arr) / sizeof(arr[0]);
int val = 100;
int accepval = Binary_Que(arr, size, val);
system("pause");
return 0;
}
3.
重复数据找到起始元素下标
线性探测
#include <stdio.h>
#include <stdlib.h>
int Binary_Que(int *cp, int size,int val)
{
int left = 0;
int right = size - 1;
int pos = -1;
int mid = 0;
while (left <= right)
{
mid = (left + right) / 2;
if (cp[mid] == val)
{
while (cp[mid] == val)
{
pos = mid;
mid--;
}
break;
}
else if (cp[mid] < val)
{
left = mid + 1;
}
else
{
right = mid - 1;
}
}
return pos;
}
int main()
{
int arr[] = { 12, 12, 12, 12, 12, 12, 12, 23, 23, 23, 23, 23, 34, 45, 56, 78, 89, 90, 100, 110, 120 };
int size = sizeof(arr) / sizeof(arr[0]);
int val = 100;
int accepval = Binary_Que(arr, size, val);
system("pause");
return 0;
}若有连续相同的数出现,在若干个相同的数找第一个数的下标,可再用二分法(更快速)
#include <stdio.h>
#include <stdlib.h>
int Binary_Que(int *cp, int size,int val)
{
int left = 0;
int right = size - 1;
int pos = -1;
int mid = 0;
while (left <= right)
{
mid = (left + right) / 2;
if (cp[mid] == val)
{
if (mid > left&&cp[mid - 1] == val)
{
right = mid - 1;
}
else
{
pos = mid;
break;
}
}
else if (cp[mid] < val)
{
left = mid + 1;
}
else
{
right = mid - 1;
}
}
return pos;
}
int main()
{
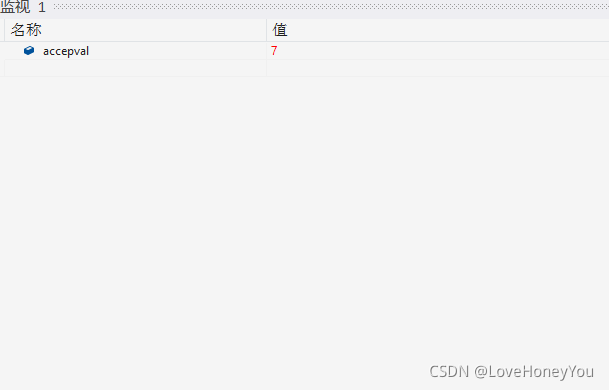
int arr[] = { 12, 12, 12, 12, 12, 12, 12, 23, 23, 23, 23, 23, 34, 45, 56, 78, 89, 90, 100, 110, 120 };
int size = sizeof(arr) / sizeof(arr[0]);
int val = 23;
int accepval = Binary_Que(arr, size, val);
system("pause");
return 0;
}
这个有点难理解,请看下图:
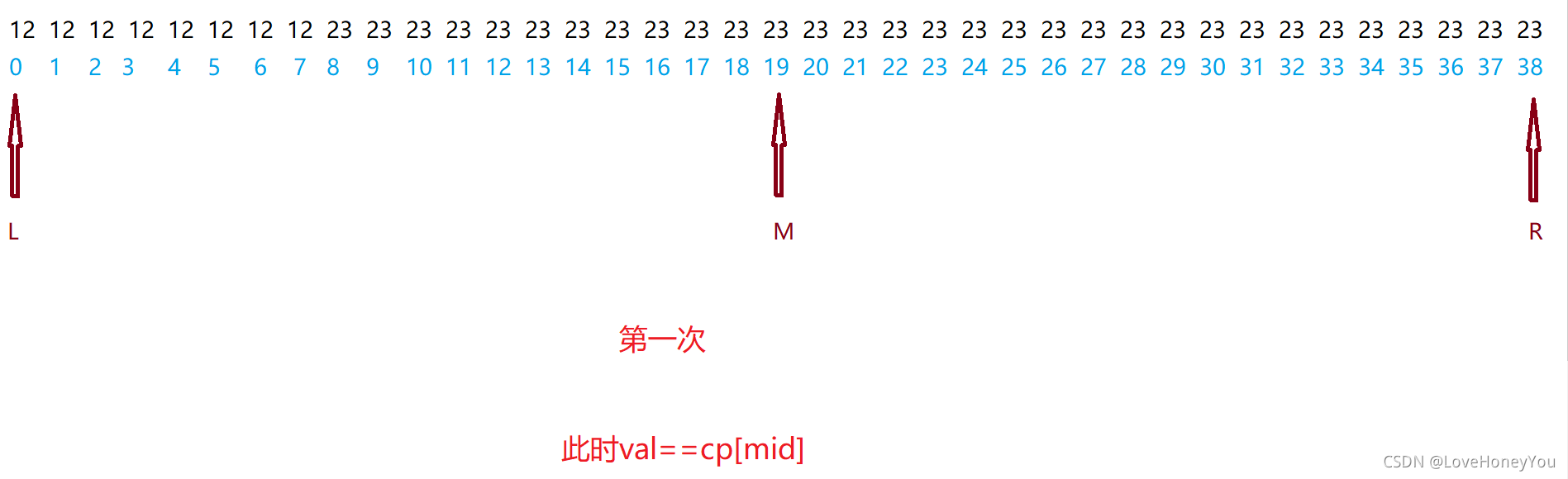
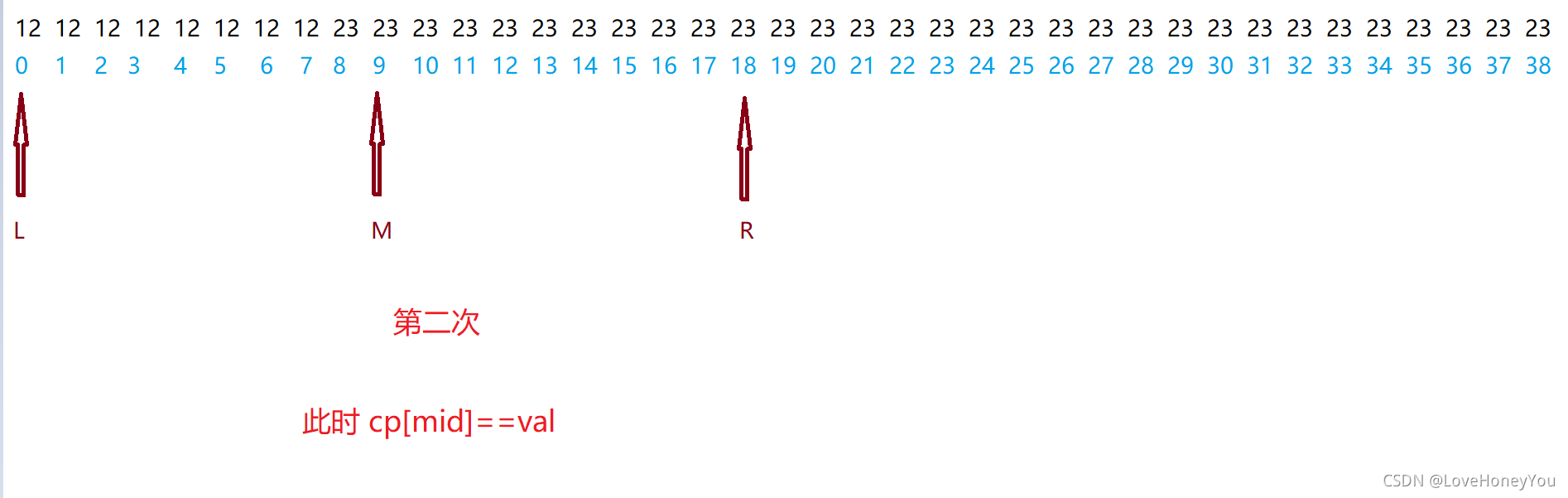




对上述代码的这个小块再稍微解析一下

假设 我们的数组元素为:
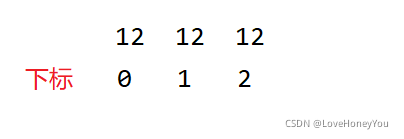
要查找的是12第一次出现的位置 ,看图解
(1)
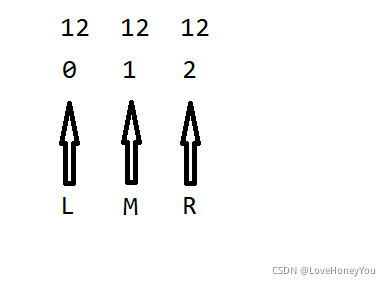
(2)
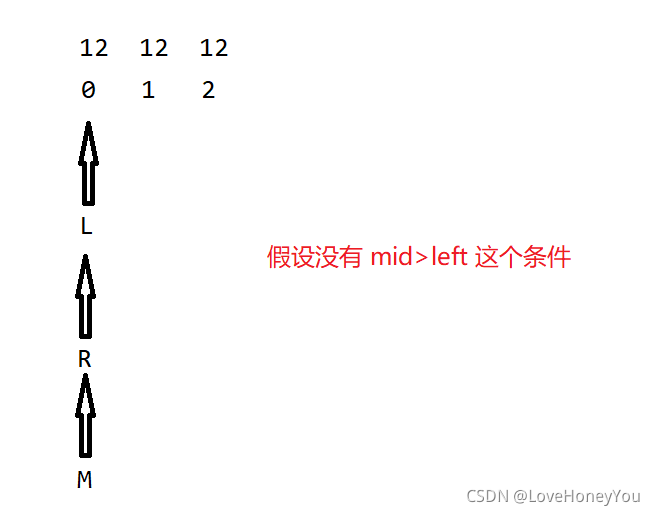
(3)
存在mid>left 这个条件时,可有效避免左越界的问题。
