UA OPTI512R 傅立叶光学导论16 Nyquist-Shannon采样定理
- 周期性采样的数学表示
- Nyquist-Shannon采样定理
因为计算机只能处理离散数据,所以即使真实信号是连续的,我们也只能采集它的一些离散样本输入计算机中做后续处理。这种用离散序列表示连续信号的操作叫做采样(sampling)。根据每次采样间隔是否均匀可以把采样分为周期性采样(periodic sampling)与非周期性采样(non-periodic sampling),这一讲讨论周期性采样。
周期性采样的数学表示
之前介绍光学中常用特殊函数时介绍了comb函数,它的定义是
c
o
m
b
(
x
)
=
∑
n
=
−
∞
+
∞
δ
(
x
−
n
)
comb(x) = \sum_{n=-\infty}^{+\infty}\delta(x-n)
comb(x)=n=−∞∑+∞δ(x−n)
根据Dirac函数的sifting property,comb函数与函数
f
(
x
)
f(x)
f(x)相乘时,作用是把
f
(
x
)
f(x)
f(x)变成序列
{
f
(
n
)
}
\{f(n)\}
{f(n)},也就是每间隔1单位做一次采样,假设我们希望的采样间隔为
Δ
\Delta
Δ,则只需要用
f
(
x
)
f(x)
f(x)与
c
o
m
b
(
x
/
Δ
)
comb(x/\Delta)
comb(x/Δ)相乘就能得到间隔为
Δ
\Delta
Δ的样本序列了。由此我们定义信号
f
(
x
)
f(x)
f(x)的采样间隔为
Δ
\Delta
Δ的采样函数(sampled function)为
f
S
(
x
)
=
f
(
x
)
⋅
(
1
Δ
c
o
m
b
(
x
/
Δ
)
)
f_S(x)=f(x) \cdot \left( \frac{1}{\Delta} comb(x/\Delta) \right)
fS(x)=f(x)⋅(Δ1comb(x/Δ))
其中
1
/
Δ
1/\Delta
1/Δ的作用是做标准化,保证采样得到的离散信号相对源信号不会被放大或者缩小,从数学上讲它的作用是保证脉冲函数的归一性
∫
−
∞
+
∞
1
Δ
δ
(
x
/
Δ
−
n
)
d
x
=
1
=
∫
−
∞
+
∞
δ
(
x
−
n
Δ
)
d
x
\int_{-\infty}^{+\infty} \frac{1}{\Delta} \delta(x/\Delta-n)dx=1=\int_{-\infty}^{+\infty} \delta(x-n\Delta)dx
∫−∞+∞Δ1δ(x/Δ−n)dx=1=∫−∞+∞δ(x−nΔ)dx,所以
f
S
(
x
)
=
∑
n
=
−
∞
+
∞
f
(
x
n
)
δ
(
x
−
x
n
)
,
x
n
=
n
Δ
f_S(x)=\sum_{n=-\infty}^{+\infty}f(x_n)\delta(x-x_n),x_n = n\Delta
fS(x)=n=−∞∑+∞f(xn)δ(x−xn),xn=nΔ
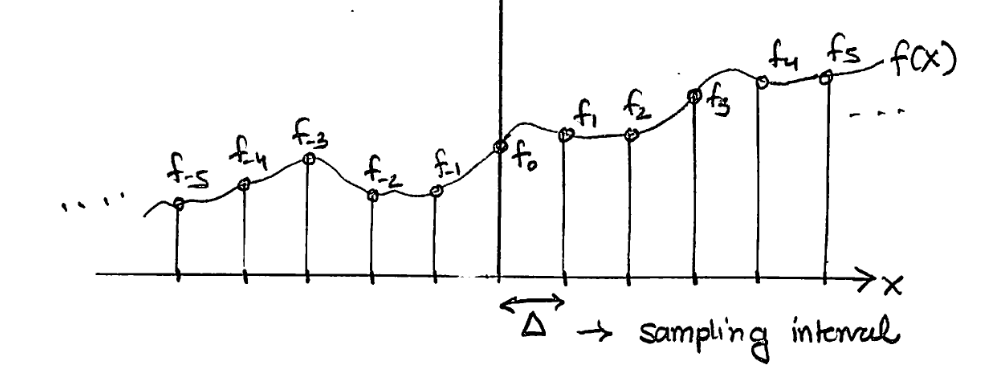
采样函数的频率谱
假设
F
(
ξ
)
=
F
[
f
(
x
)
]
F(\xi)=\mathcal{F}[f(x)]
F(ξ)=F[f(x)],则
F
S
(
ξ
)
=
∑
n
=
−
∞
+
∞
F
(
ξ
−
n
ξ
S
)
F_S(\xi)=\sum_{n=-\infty}^{+\infty}F(\xi - n\xi_S)
FS(ξ)=n=−∞∑+∞F(ξ−nξS)
其中
ξ
S
=
1
Δ
\xi_S=\frac{1}{\Delta}
ξS=Δ1被称为采样频率,这个结果说明采样函数的频率谱就是源信号的频率谱平移
{
n
ξ
S
}
\{n\xi_S\}
{nξS}后的叠加。
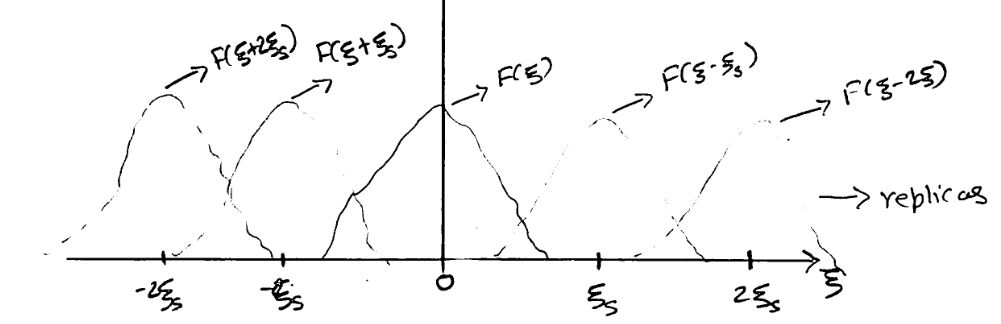
用卷积定理可以得到上述结果:
F
S
(
ξ
)
=
F
[
f
(
x
)
⋅
(
1
Δ
c
o
m
b
(
x
/
Δ
)
)
]
=
F
[
f
(
x
)
]
∗
F
[
1
Δ
c
o
m
b
(
x
/
Δ
)
]
=
F
(
ξ
)
∗
c
o
m
b
(
ξ
/
ξ
S
)
=
F
(
ξ
)
∗
∑
n
=
−
∞
+
∞
δ
(
ξ
−
n
ξ
S
)
=
∑
n
=
−
∞
+
∞
F
(
ξ
−
n
ξ
S
)
\begin{aligned}F_S(\xi) &=\mathcal{F}\left[f(x) \cdot \left( \frac{1}{\Delta} comb(x/\Delta) \right)\right] \\ & = \mathcal{F}[f(x)] * \mathcal{F} \left[ \frac{1}{\Delta} comb(x/\Delta) \right] \\ & = F(\xi) * comb(\xi/\xi_S) \\ & = F(\xi) * \sum_{n=-\infty}^{+\infty} \delta(\xi-n\xi_S) \\ &= \sum_{n=-\infty}^{+\infty}F(\xi - n\xi_S)\end{aligned}
FS(ξ)=F[f(x)⋅(Δ1comb(x/Δ))]=F[f(x)]∗F[Δ1comb(x/Δ)]=F(ξ)∗comb(ξ/ξS)=F(ξ)∗n=−∞∑+∞δ(ξ−nξS)=n=−∞∑+∞F(ξ−nξS)
Nyquist-Shannon采样定理
Band-limited Function 在某个区间内有非零频率谱的函数被称为Band-limited Function,用
f
B
(
x
)
f_B(x)
fB(x)来表示,其中
B
B
B代表带宽,则它的数学定义为
F
B
(
ξ
)
=
F
[
f
B
(
x
)
]
{
>
0
,
∣
ξ
∣
≤
B
2
=
0
,
∣
ξ
∣
>
B
2
F_B(\xi) = \mathcal{F}[f_B(x)] \begin{cases} >0,|\xi| \le \frac{B}{2} \\ =0,|\xi|>\frac{B}{2}\end{cases}
FB(ξ)=F[fB(x)]{>0,∣ξ∣≤2B=0,∣ξ∣>2B
采样定理 这个定理想讨论的问题是离散的样本序列能不能代表完整的信号,毕竟把连续信号用离散序列表示本身是有信息损失的。这个问题在Shannon之前,Whittaker、Nyquist等人已经讨论过了,到Shannon时候,他建立了完整的理论,也就是现在非常有用的信息论,他认为源信号是Band-limited Function时,只要采样频率大于源信号频率谱的带宽( ξ S > B \xi_S>B ξS>B),那么采样得到的离散信号就可以完美得重构出源信号。
Shannon的思想可以用一个很简单的filter论证,
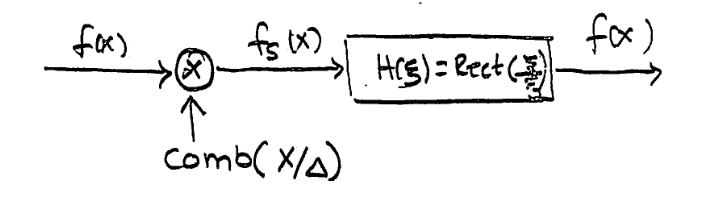
现在我们有采样函数的频谱
F
S
(
ξ
)
F_S(\xi)
FS(ξ),引入一个滤波器
F
[
h
(
x
)
]
=
H
(
ξ
)
h
(
x
)
=
B
s
i
n
c
(
B
)
,
H
(
ξ
)
=
r
e
c
t
(
ξ
/
B
)
\mathcal{F}[h(x)]=H(\xi) \\ h(x)=Bsinc(B),H(\xi)=rect(\xi/B)
F[h(x)]=H(ξ)h(x)=Bsinc(B),H(ξ)=rect(ξ/B)
采样函数的频谱与这个滤波器作用后的结果为
F
^
(
ξ
)
=
F
S
(
ξ
)
H
(
ξ
)
=
∑
n
=
−
∞
+
∞
F
(
ξ
−
n
ξ
S
)
H
(
ξ
)
\hat F(\xi)=F_S(\xi)H(\xi)=\sum_{n=-\infty}^{+\infty}F(\xi - n\xi_S)H(\xi)
F^(ξ)=FS(ξ)H(ξ)=n=−∞∑+∞F(ξ−nξS)H(ξ)
因为
H
(
ξ
)
=
r
e
c
t
(
ξ
/
B
)
=
0
H(\xi)=rect(\xi/B)=0
H(ξ)=rect(ξ/B)=0,
∀
∣
ξ
∣
≥
B
/
2
\forall |\xi| \ge B/2
∀∣ξ∣≥B/2,也就是说在一个带宽以外的频谱无法通过滤波器,只有
n
=
0
n=0
n=0时的频谱
F
(
ξ
)
F(\xi)
F(ξ)可以保留下来,所以
ξ
S
>
B
\xi_S>B
ξS>B时,
F
^
(
ξ
)
=
F
(
ξ
)
\hat F(\xi)=F(\xi)
F^(ξ)=F(ξ)
也即通过采样函数可以完美还原出源信号的频谱。
根据卷积定理,
f
^
(
x
)
=
F
−
1
[
F
S
(
ξ
)
H
(
ξ
)
]
=
f
S
(
x
)
∗
h
(
x
)
=
∑
n
=
−
∞
+
∞
f
(
x
n
)
δ
(
x
−
x
n
)
∗
B
s
i
n
c
(
B
x
)
=
B
∑
n
=
−
∞
+
∞
f
(
x
n
)
s
i
n
c
(
B
(
x
−
x
n
)
)
\hat f(x)=\mathcal{F}^{-1}[F_S(\xi)H(\xi)] = f_S(x)*h(x) \\ =\sum_{n=-\infty}^{+\infty}f(x_n)\delta(x-x_n) * B sinc(Bx)=B \sum_{n=-\infty}^{+\infty}f(x_n) sinc(B(x-x_n))
f^(x)=F−1[FS(ξ)H(ξ)]=fS(x)∗h(x)=n=−∞∑+∞f(xn)δ(x−xn)∗Bsinc(Bx)=Bn=−∞∑+∞f(xn)sinc(B(x−xn))
相当于用sinc曲线连接离散序列 { f ( x n ) } \{f(x_n)\} {f(xn)}做插值来还原 f ( x ) f(x) f(x),当 ξ S > B \xi_S>B ξS>B时, f ^ ( x ) ∝ f ( x ) \hat f(x) \propto f(x) f^(x)∝f(x)。
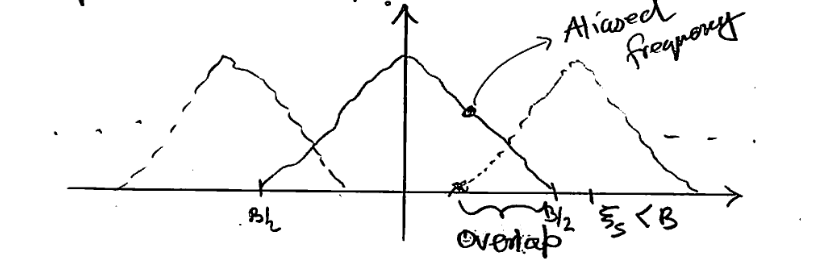
如果
ξ
S
<
B
\xi_S<B
ξS<B,则组成
F
S
(
ξ
)
F_S(\xi)
FS(ξ)的各段频域会重叠,用
H
(
ξ
)
H(\xi)
H(ξ)这个滤波器得到的频域包含左右两端重叠部分,导致还原出的频谱
F
^
(
ξ
)
\hat F(\xi)
F^(ξ)与源信号频域
F
(
ξ
)
F(\xi)
F(ξ)不一致。
