1 简介
车辆路径问题(Vehicle Routing Problem, VRP)是物流配送过程中的关键问题之一,随着物流配送行业竞争日益激烈和客户对物流配送时效性要求越来越高,对车辆路径问题的研究,尤其是对带时间窗车辆路径问题(Vehicle Routing Problem With Time Windows, VRPTW)的研究,不仅可以帮助外卖行业提高服务水平,为客户提供快捷,准时,安全,舒适的服务,而且有助于商家节约运输成本,提高骑手利用效率,实现资源的合理配置,汲取"第三利润源泉"的财富,因此研究带时间窗车辆路径问题具有重要的现实意义. 本文正是基于以上背景对带时间窗的车辆路径优化问题进行了相关研究.论文从旅行商问题出发,通过分析带时问窗车辆路径优化问题的基本理论,对可用于求解VRPTW的各种优化算法进行了对比,确定了遗传算法作为本文VRPTW求解算法.在此基础上,考虑配送距离,配送及时性以及配送车辆数对配送成本的影响,构建了以配送总成本最小化为目标的带有惩罚函数的VRPTW(订单不变化)优化模型,并设计了适合于该模型求解的染色体编码方式以及遗传算子等.最后,应用算例进行了仿真试验,利用MATLAB软件分别计算基本遗传算法的最优目标函数值与最优配送路径方案,通过对试验结果的对比分析,验证了本文所建模型及求解算法的合理性和有效性.
2 部分代码
clear
clc
close all
tic
NIND=1000; %种群大小
MAXGEN=50; %迭代次数
Pc=0.9; %交叉概率
Pm=0.05; %变异概率
GGAP=0.9; %代沟(Generation gap)
N=cusnum;
%% 初始化种群
[s,g,sj,gk,Chrom]=init(cusnum,NIND,F); %构造初始解
%% 输出随机解的路线和总距离
disp('初始种群中的一个随机值:')
[VC,TD,violate_cus]=decode(Chrom(1,:),cusnum,a,b,L,dist,chesu,bl);
% disp(['总距离:',num2str(TD)]);
disp(['车辆行驶总距离:',num2str(TD)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
%% 优化
gen=1;
figure;
hold on;box on
xlim([0,MAXGEN])
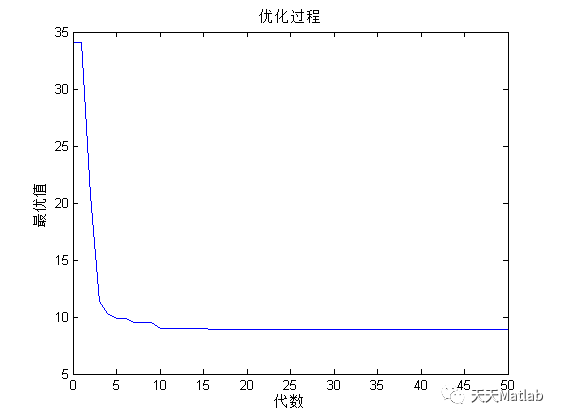
title('优化过程')
xlabel('代数')
ylabel('最优值')
[ObjV,bsv,gs,w1,w2]=calObj(Chrom,cusnum,a,b,L,dist,alpha,belta,belta2,chesu,bl); %计算种群目标函数值
preObjV=min(ObjV);
%%
while gen<=MAXGEN
%% 计算适应度
[ObjV,bsv,gs,w1,w2]=calObj(Chrom,cusnum,a,b,L,dist,alpha,belta,belta2,chesu,bl); %计算种群目标函数值
preObjV=min(ObjV);
FitnV=Fitness(ObjV);
%% 选择
[bestVC,bestTD,best_viocus]=decode(Chrom(minInd(1),:),cusnum,a,b,L,dist,chesu,bl);
disp(['车辆行驶总距离:',num2str(bestTD)]);
fprintf('\n')
%% 更新迭代次数
gen=gen+1 ;
end
%% 画出最优解的路线图
[ObjV,bsv,gs,w1,w2]=calObj(Chrom,cusnum,a,b,L,dist,alpha,belta,belta2,chesu,bl); %计算种群目标函数值
[minObjV,minInd]=min(ObjV);
%% 输出最优解的路线和总距离
disp('最优解:')
bestChrom=Chrom(minInd(1),:);
[bestVC,bestTD,best_viocus]=decode(bestChrom,cusnum,a,b,L,dist,chesu,bl);
disp(['车辆行驶总距离:',num2str(bestTD)]);
disp('-------------------------------------------------------------')
% %% 画出最终路线图
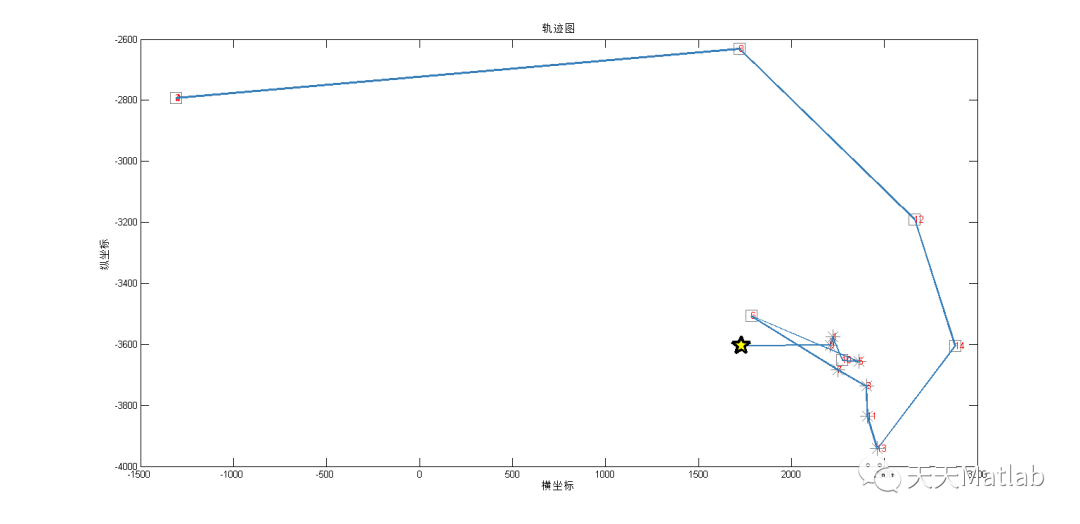
draw_Best(bestVC,zuobiao,b,bsv,gk,sj,cusnum,F);
% save
% toc
3 仿真结果
4 参考文献
[1]潘立军, 符卓. 求解带时间窗取送货问题的遗传算法[J]. 2021(2012-1):120-126.
部分理论引用网络文献,若有侵权联系博主删除。

