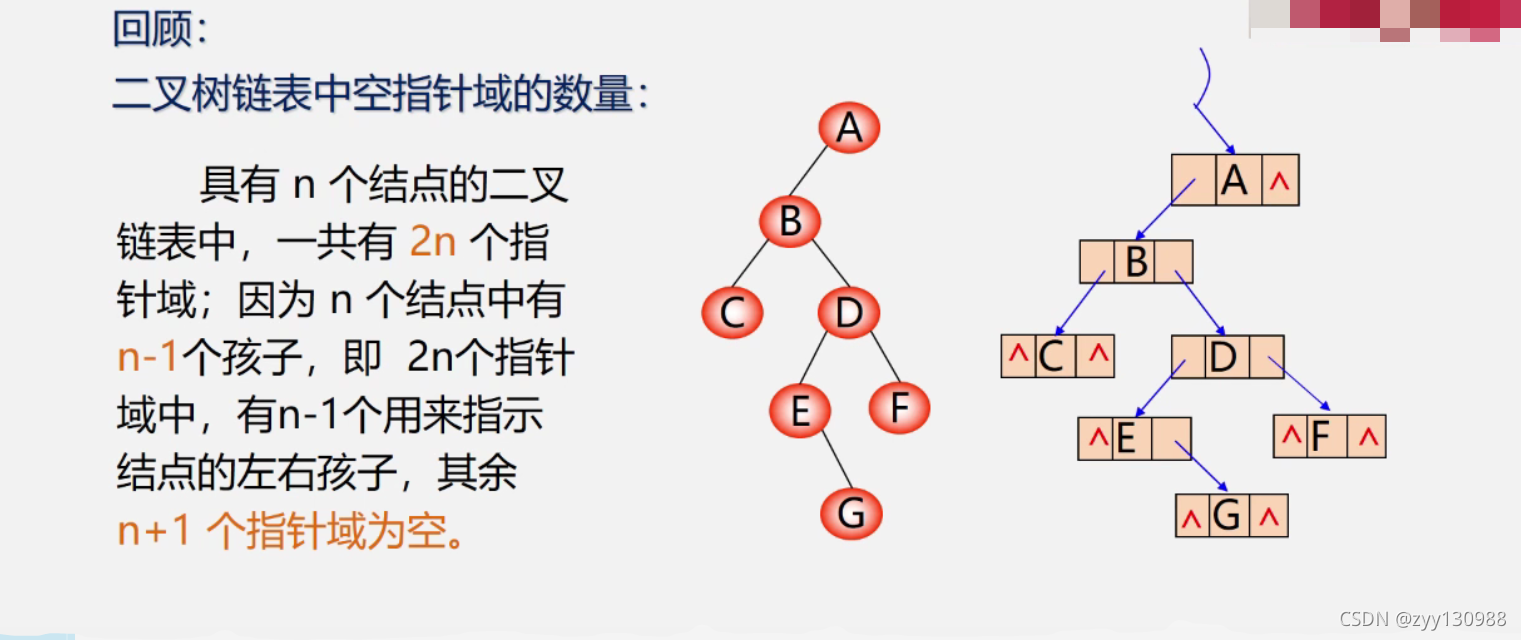
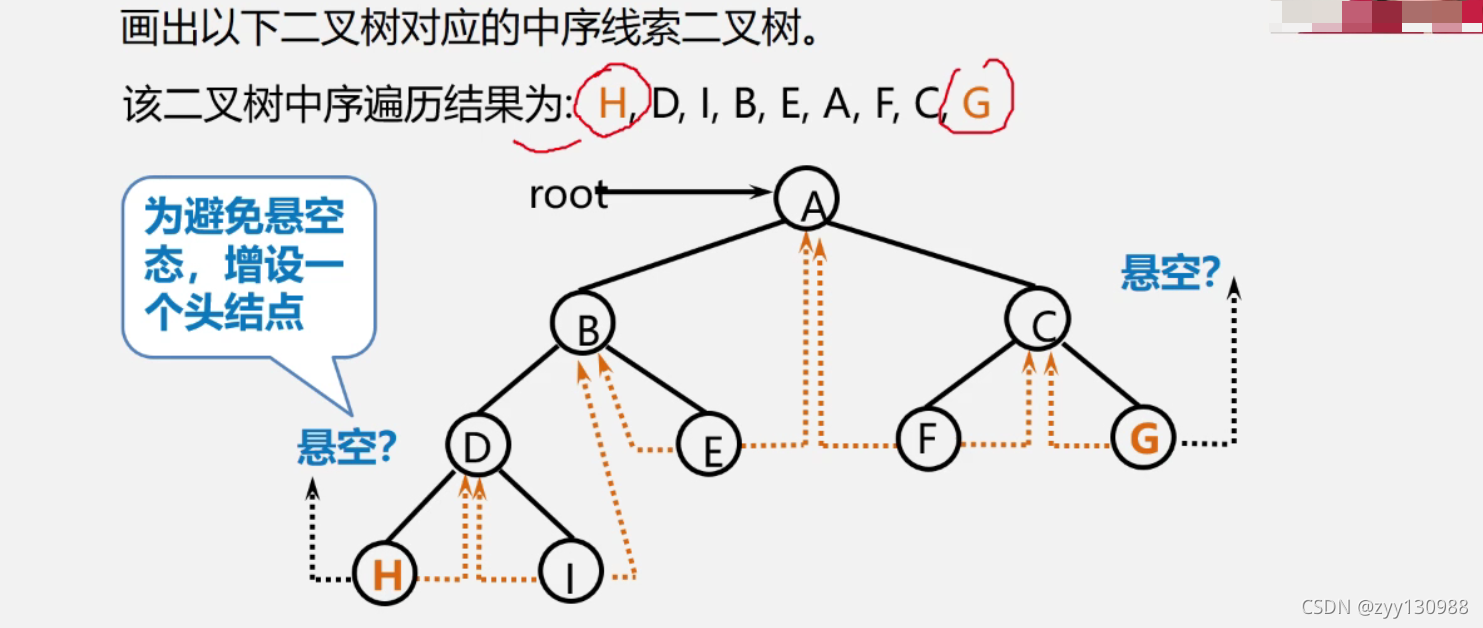
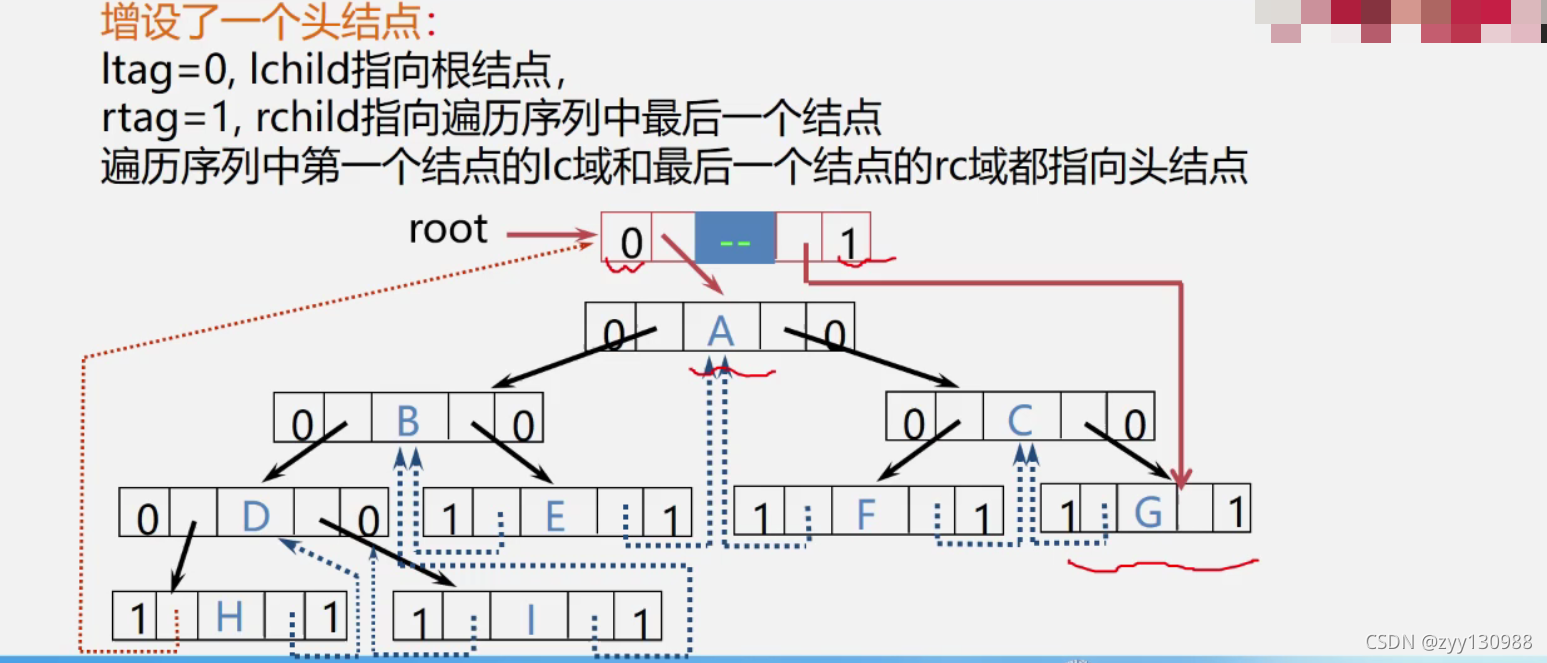
遍历二叉树与线索二叉树
- 遍历二叉树算法描述
- 先序遍历二叉树
- 中序遍历二叉树
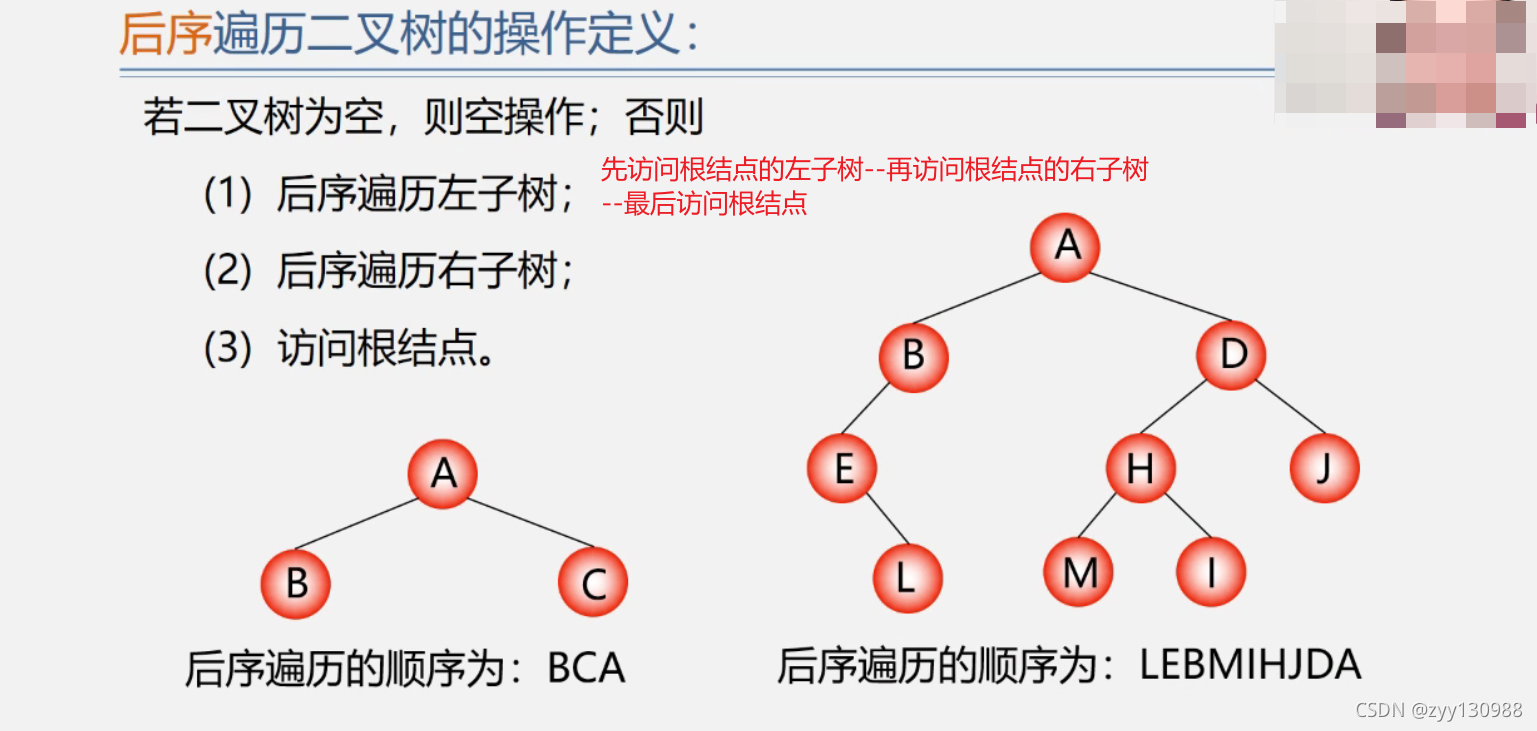
- 后序遍历二叉树
- 例题
- 根据遍历序列确定二叉树
- 根据先序和中序确定二叉树
- 根据后序和中序确定二叉树
- 线索二叉树


遍历二叉树算法描述
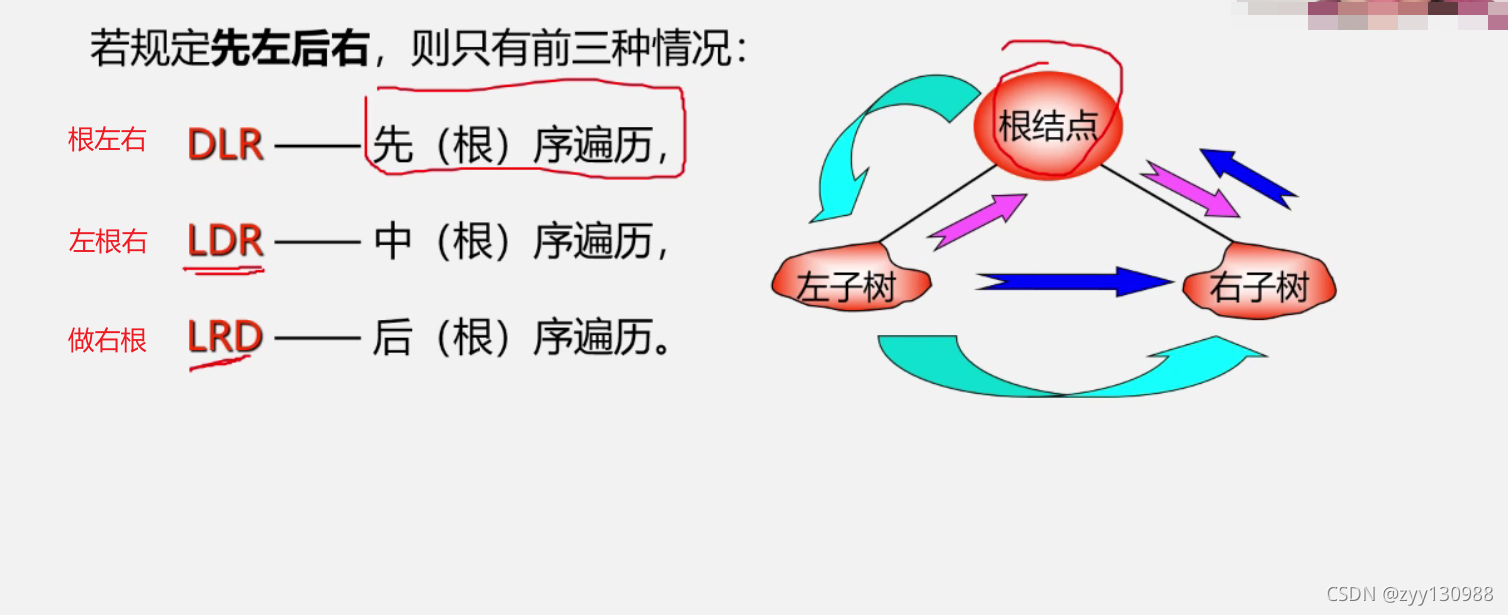

先序遍历二叉树
访问根结点A–访问根结点A的左子树B–访问根结点B的左子树E–访问根结点E的左子树(空)
–根结点E的右子树L–访问根结点L的左子树(空)–访问根结点L的右子树(空)
–访问根结点B的右子树(空)–访问根结点A的右子树D–访问根结点D的左子树H
–访问根结点H的左子树M–访问根结点M的左子树(空)–访问根结点M的右子树(空)–访问根结点H的右子树I
–访问根结点I的左子树(空)–访问根结点I的右子树(空)–访问根结点D的右子树J
–访问根结点J的左子树(空)–访问根结点J的右子树(空)–完毕

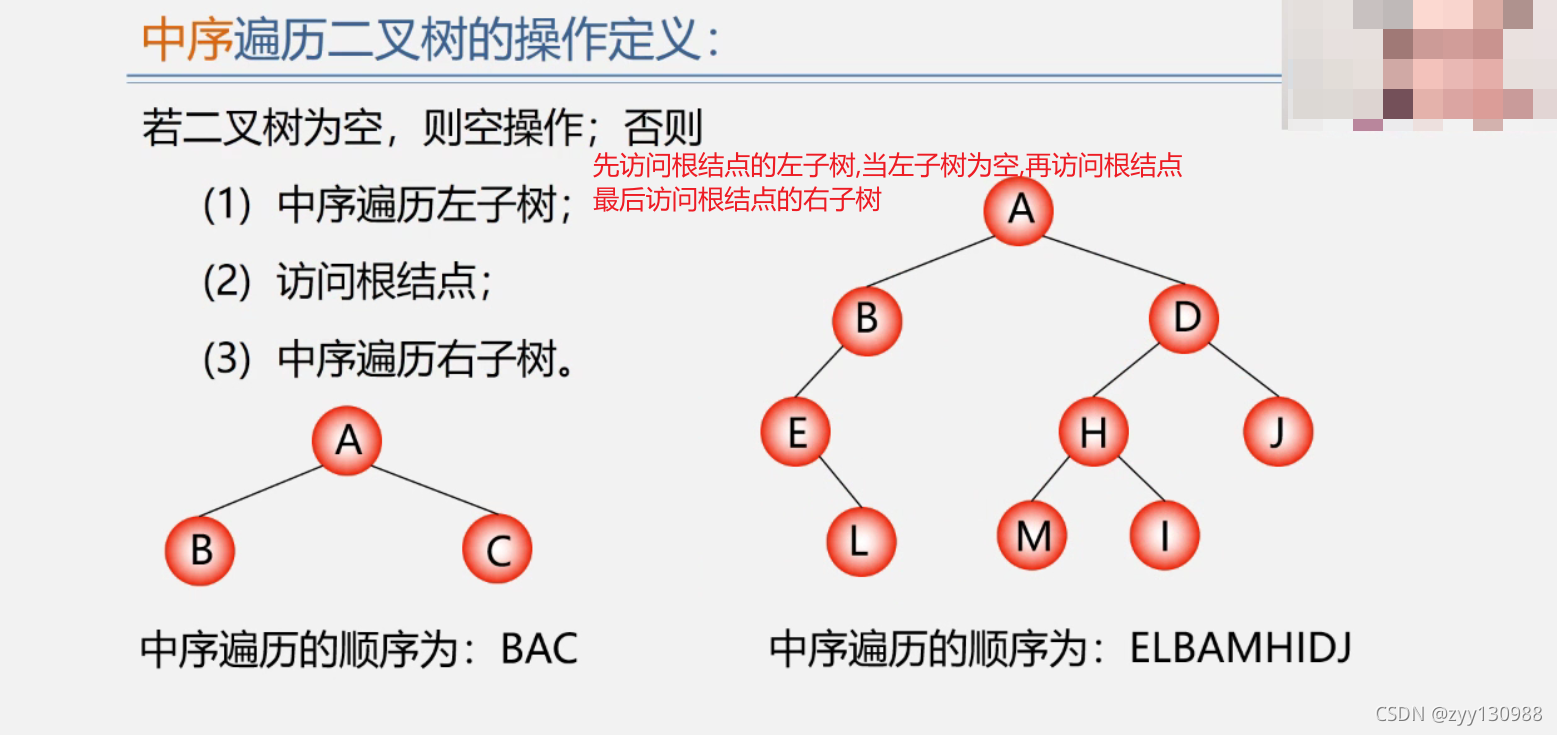
中序遍历二叉树
访问根结点A的左子树B–访问根结点B的左子树E(空)–访问根结点E–访问根结点E的右子树L–
访问根结点L的左子树(空)–访问根结点L–访问根结点L的右子树(空)–访问根结点B
–访问根结点B的右子树(空)–访问根结点A–访问根结点A的右子树D–访问根结点D的左子树H
–访问根结点H的左子树M–访问根结点M的左子树(空)–访问根结点M–访问根结点M的右子树(空)
–访问根结点H–访问根结点H的右子树I–访问I结点的左子树(空)–访问根结点I
–访问根结点I的右子树(空)–访问根结点D–访问根结点D的右子树J–访问根结点J的左子树(空)
–访问根结点J–访问根结点J的右子树(空)–返回A–完毕
后序遍历二叉树
访问A结点的左子树B–访问根结点B的左子树E–访问根结点E的左子树(空)–访问根结点E的右子树L
–访问根结点L的左子树(空)–访问根结点L的右子树(空)–访问根结点L–访问根结点E
–访问根结点B的右子树(空)–访问根结点B–访问根结点A的右子树D–访问根结点D的左子树H
–访问根结点H的左子树M–访问根结点M的左子树(空)–访问根结点M的右子树(空)–访问根结点M
–访问根结点H的右子树I–访问根结点I的左子树(空)–访问根结点I的右子树(空)–访问根结点I
–访问根结点H–访问根结点D的右子树J–访问根结点J的左子树(空)–访问根结点J的右子树(空)
–访问根结点J–访问根结点D–访问根结点A–完毕
例题
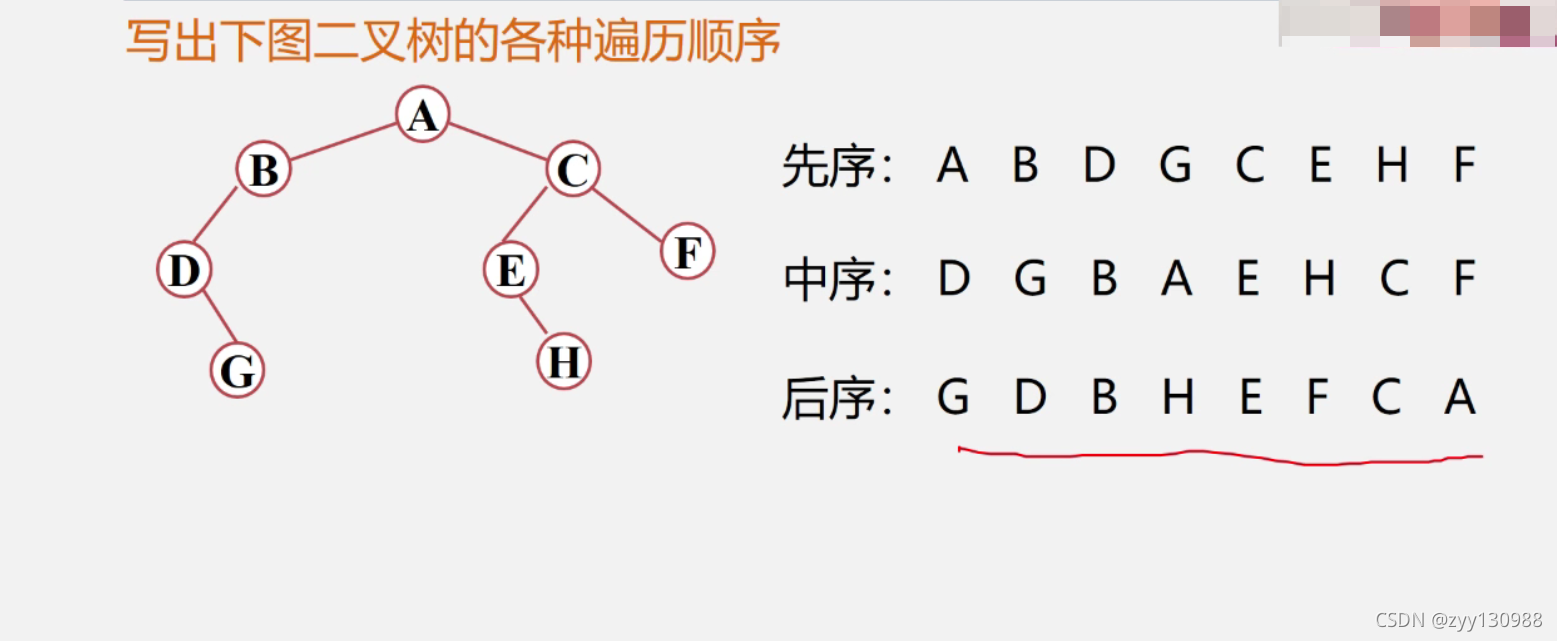

根据遍历序列确定二叉树
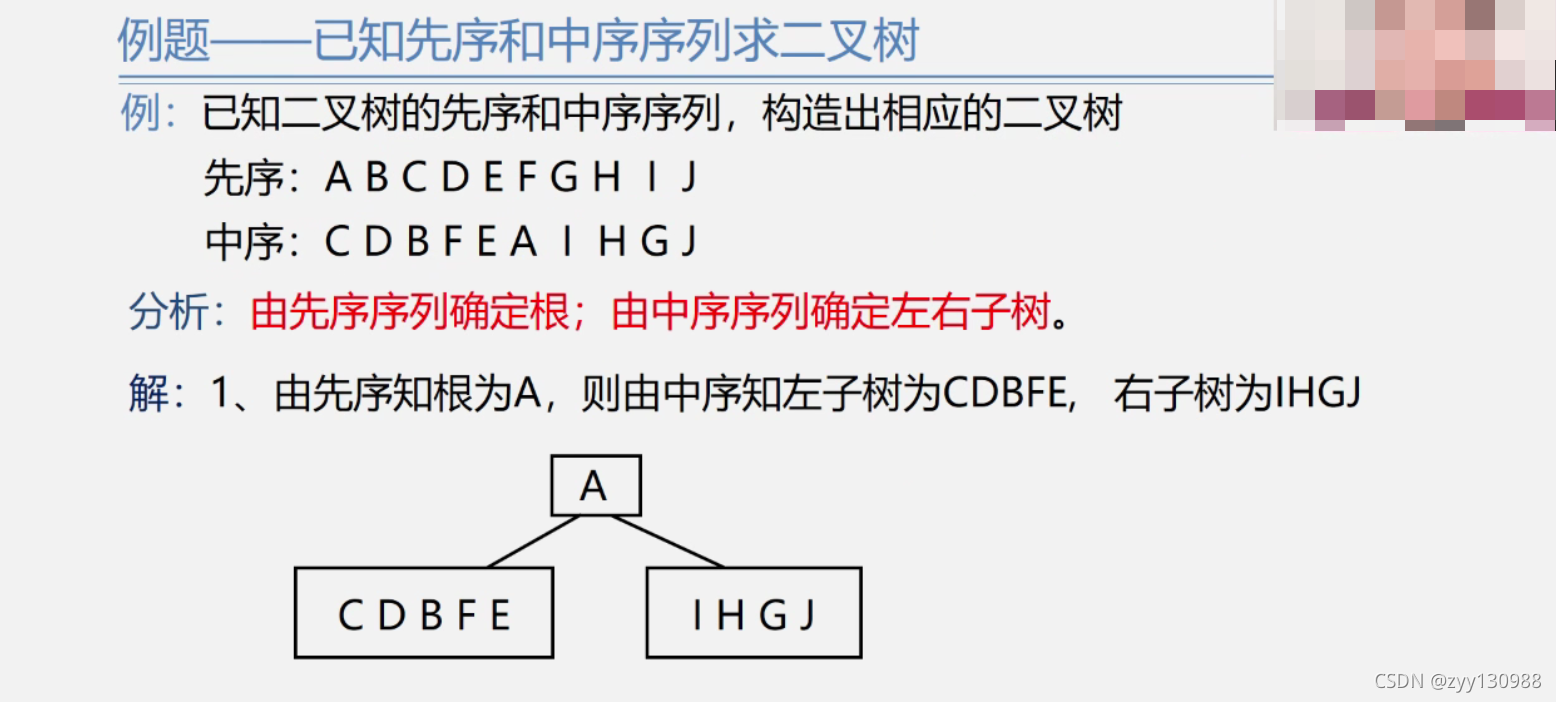
根据先序和中序确定二叉树
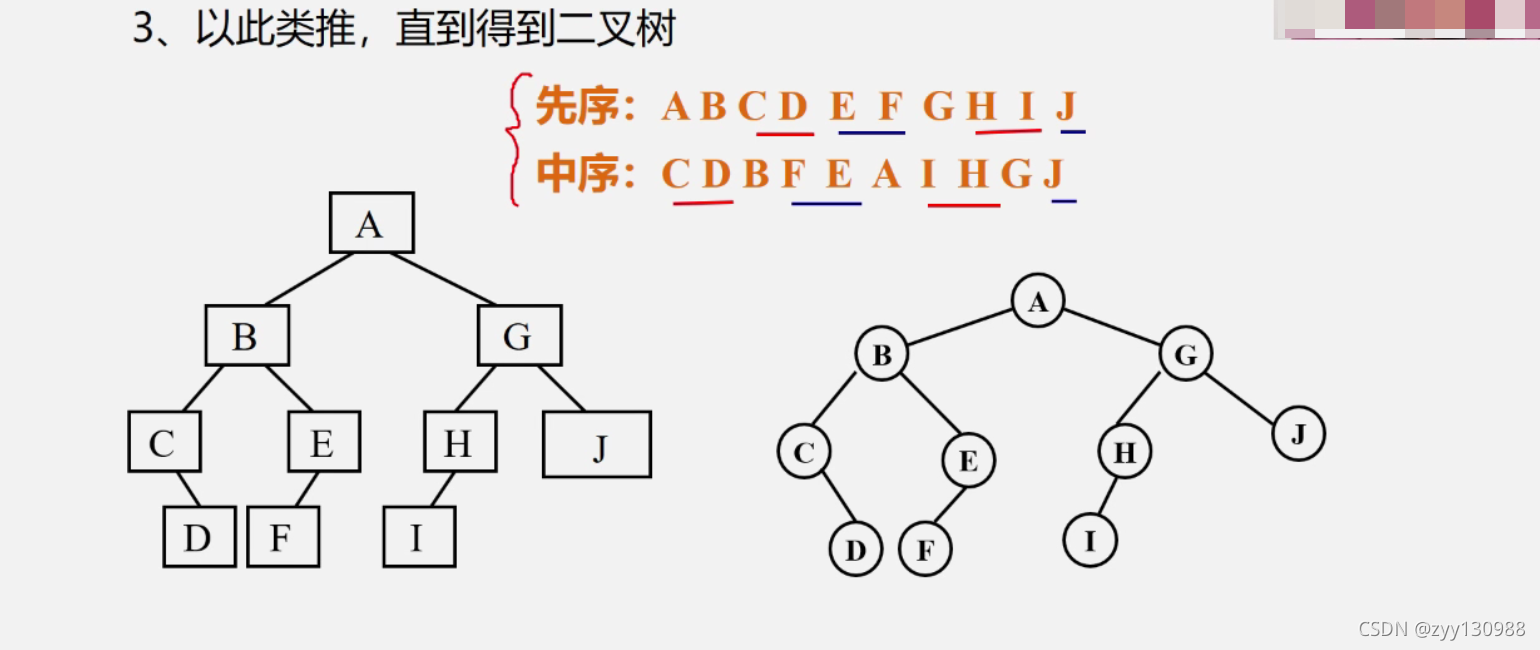
先序: A B C D E F G H I J
中序: C D B F E A I H G J
1.根据先序可以确定A是根结点
2.先序是根左右,中序是左根右,可以确定B是根结点A的左根结点,G是根结点A的右根结点
此时
左结点: B C D E F
右节点: G H I J
左节点:
3.在中序里可以看到B将C D 和 F E 分为了两半,因此,CD 为B左节点 FE为B的右节点
在先序中可以看到D为C的某个结点,而在中序可以发现D在C的右边,因此 D为C的右节点
在先序中可以看到F为E的某个结点,而在中序可以发现F在E的左边,因此 F为E的左节点
右节点:
在中序里可以看到G将I H 和 J 分为了两半,因此,I H 为G左节点 J为G的右节点
在先序中可以看到I为H的某个结点,而在中序可以发现I在H的左边,因此 I为H的左节点
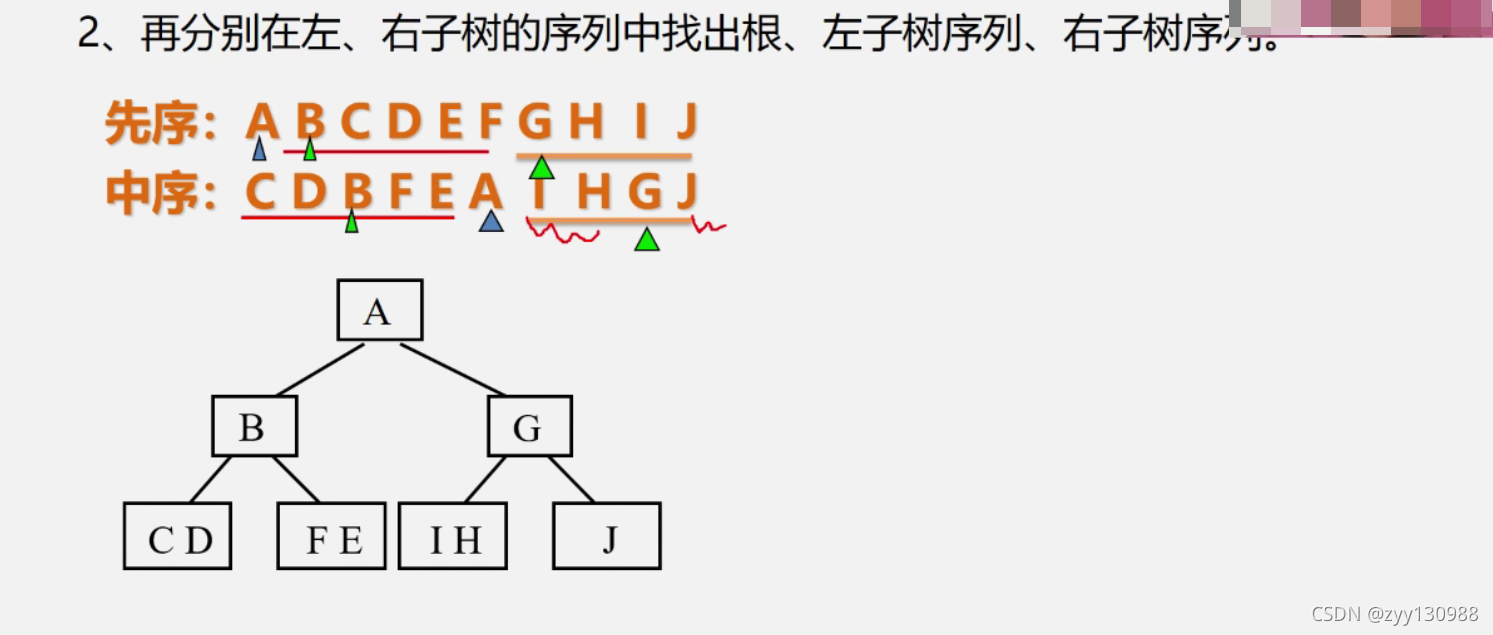
根据后序和中序确定二叉树
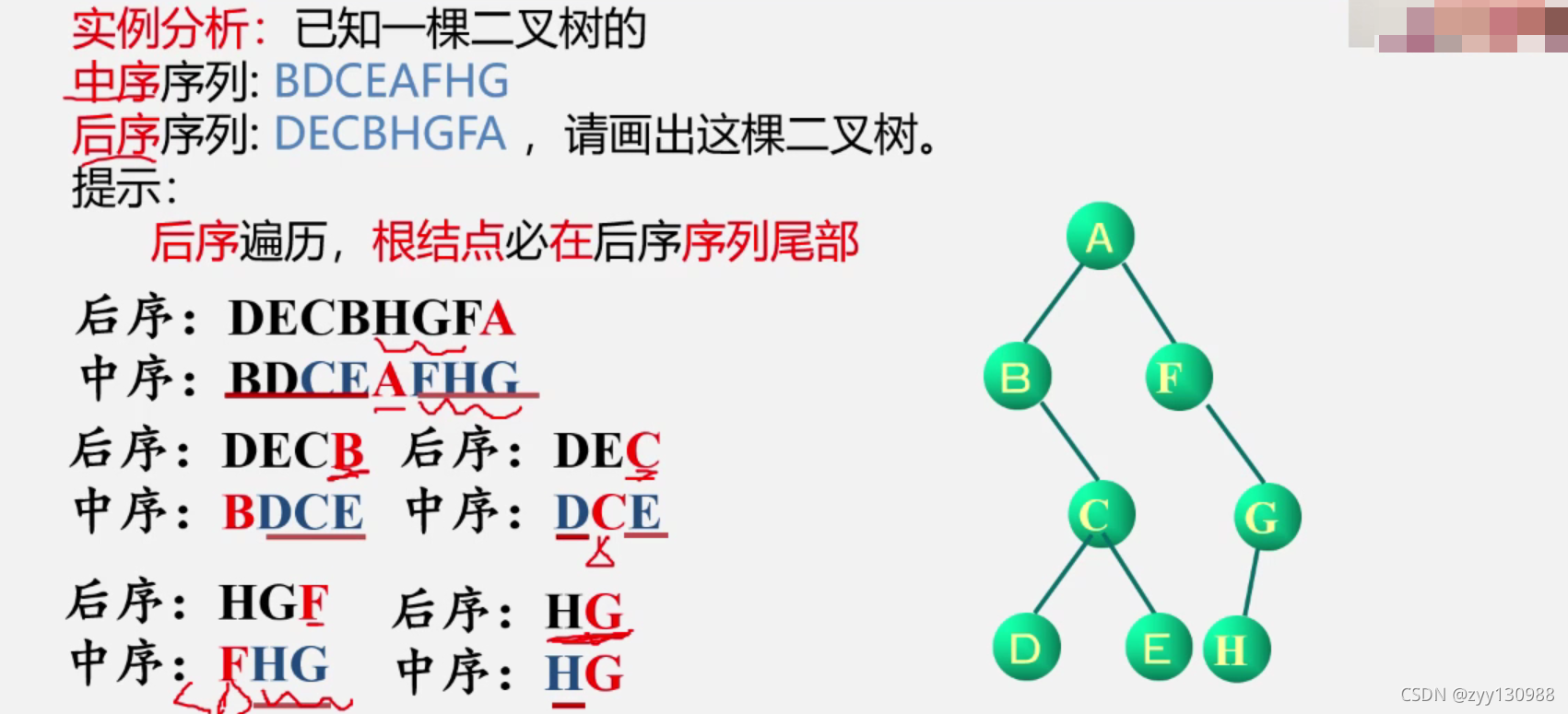
后序: D E C B H G F A 左右根
中序: B D C E A F H G 左根右
1.因为后序最后一个节点一定是根结点,所以A是整个树的根结点,
又根据中序可得
左结点: B D C E
右结点: F H G
A的左节点
后序 D E C B
中序 B D C E
2.因为后序最后一个结点一定是根结点,所以B是A的左结点,
根据中序可以发现 :B D C 在B节点的右边,所以B节点的左边为空,B D C 为B节点的右结点
后序 D E C
中序 D C E
3.因为后序最后一个结点一定是根结点,所以C是B的右结点,
根据中序可以发现 :D在C的左边,E在C的右边,所以D是C的左结点,E是C的右结点
A的右结点
后序 H G F
中序 F H G
4.因为后序最后一个结点一定是根结点,所以F是A的右结点,
根据中序可以发现 :H,G在F的右边,所以F的左节点为空,右节点为H,G
后序 H G
中序 H G
5.因为后序最后一个结点一定是根结点,所以G是F的右结点,
根据中序可以发现 :H在G的左边,所以H是G的左节点,G的右节点为空
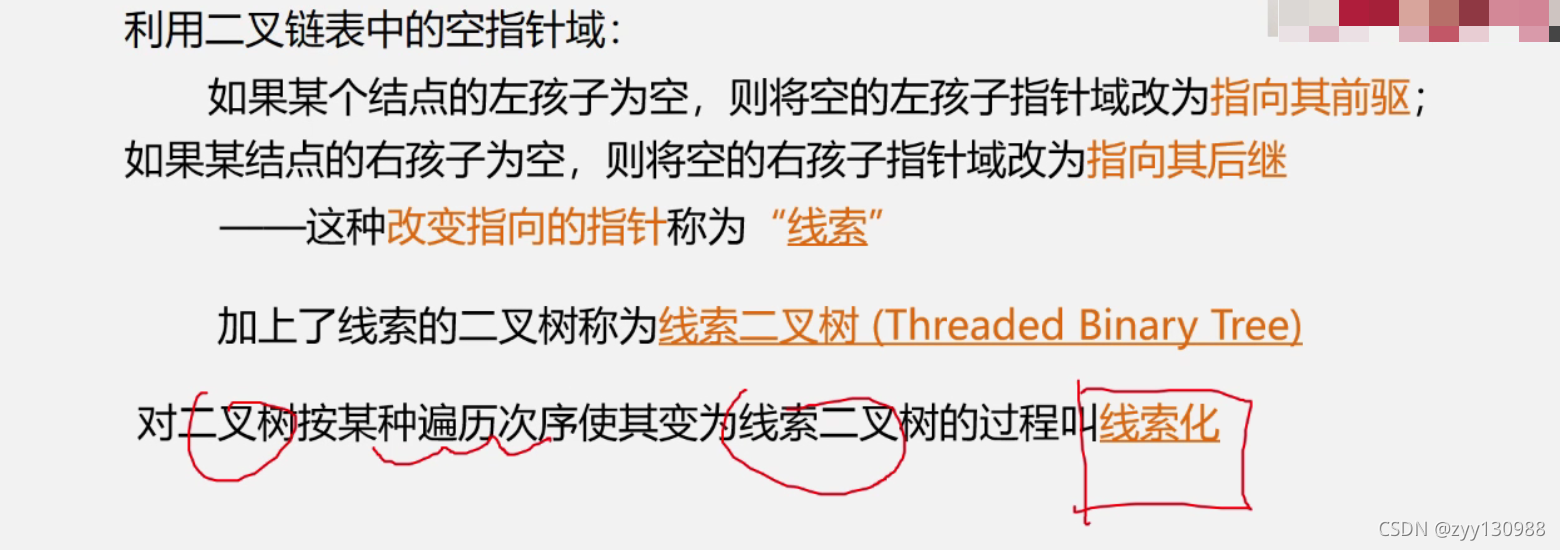
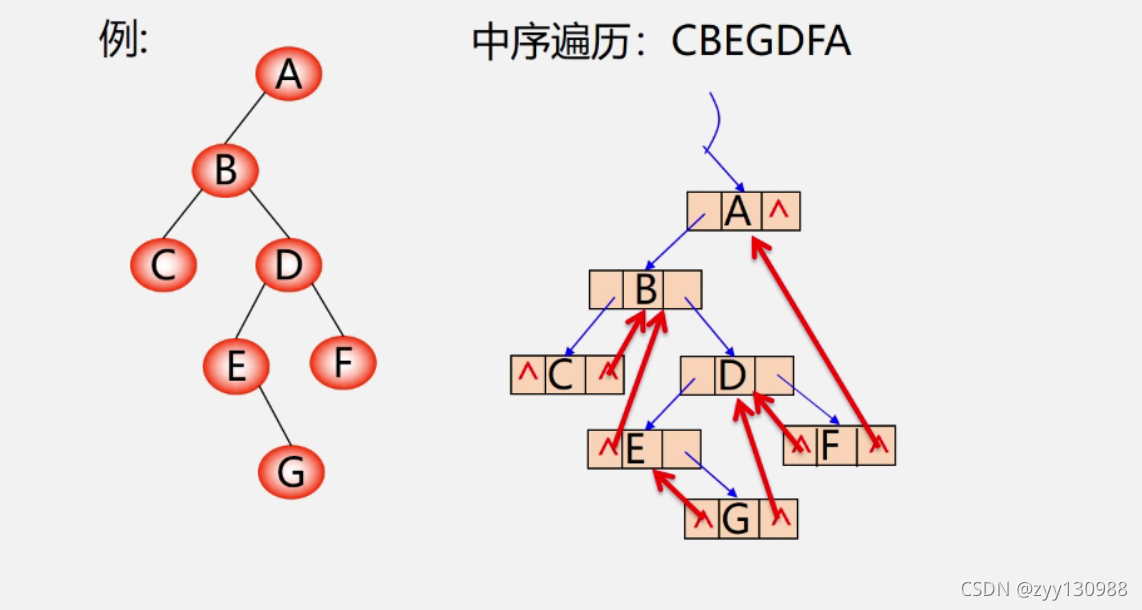
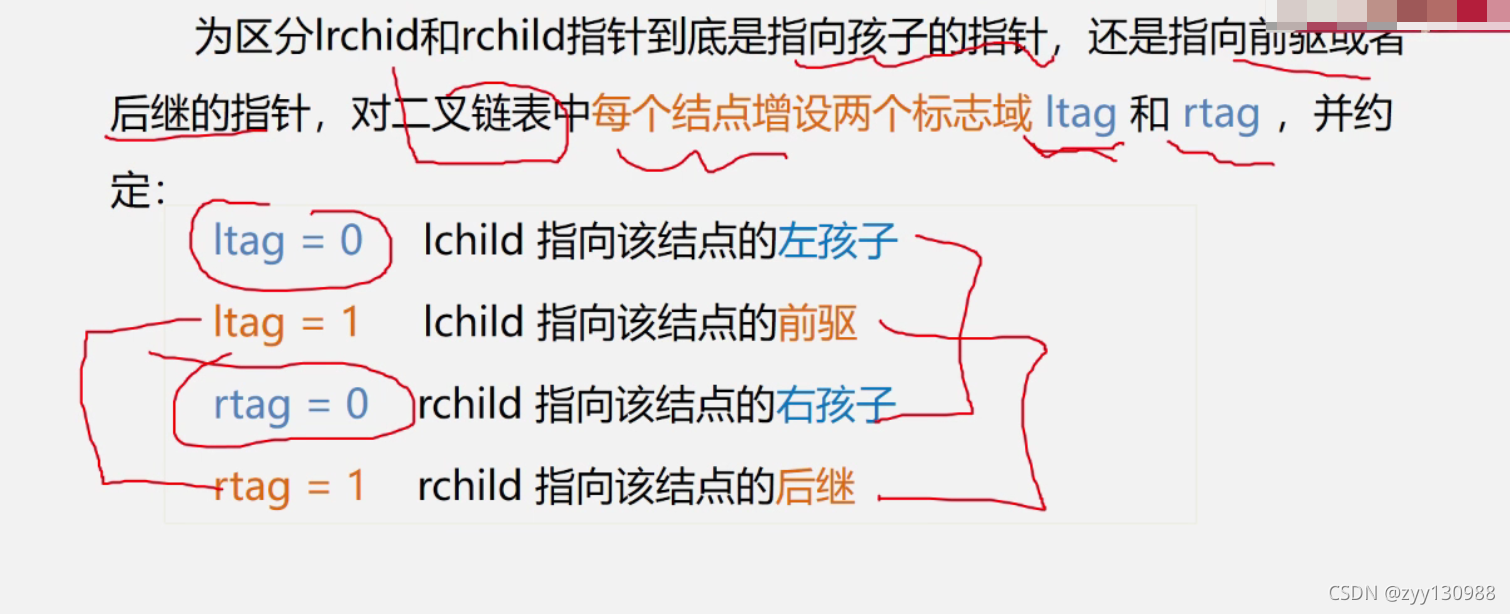
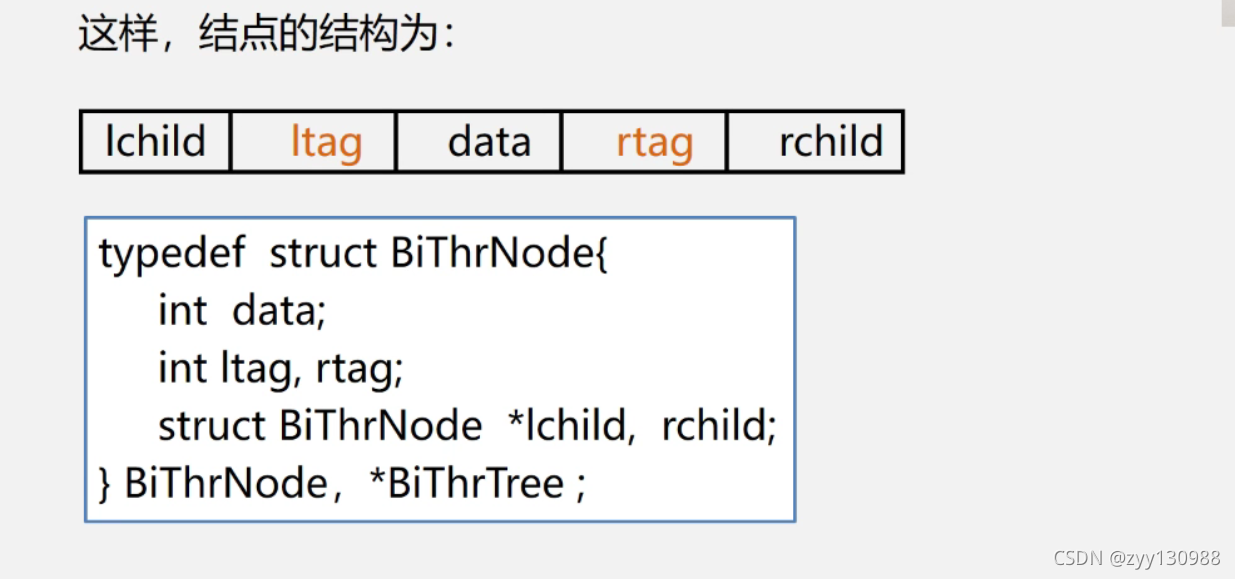
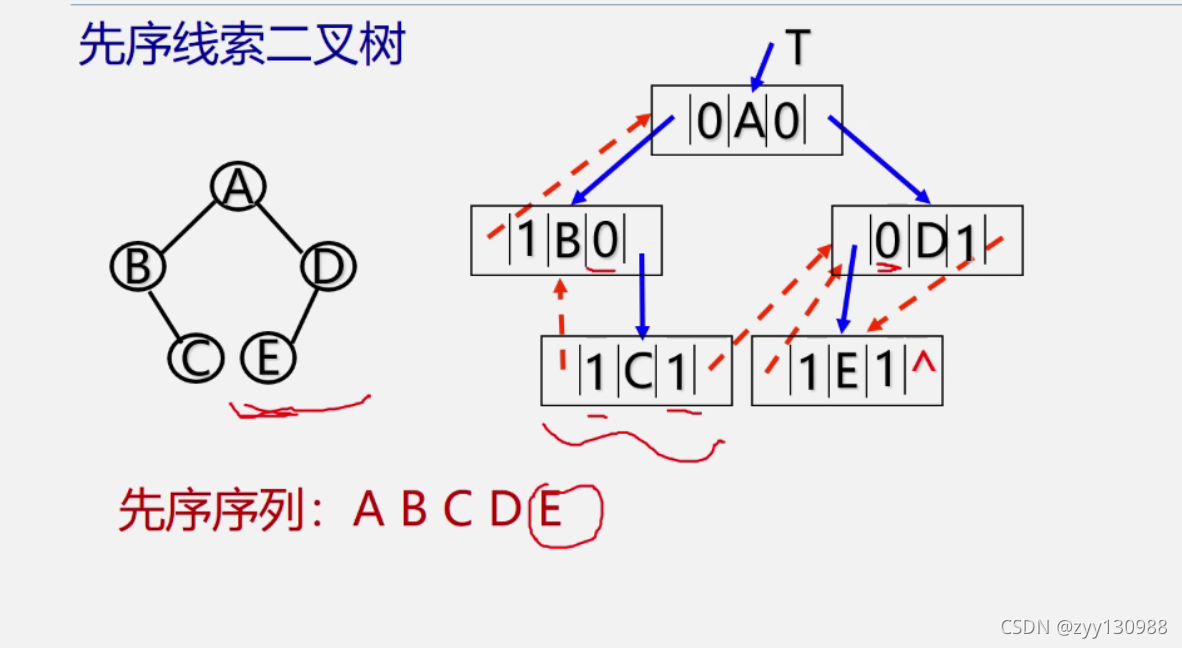
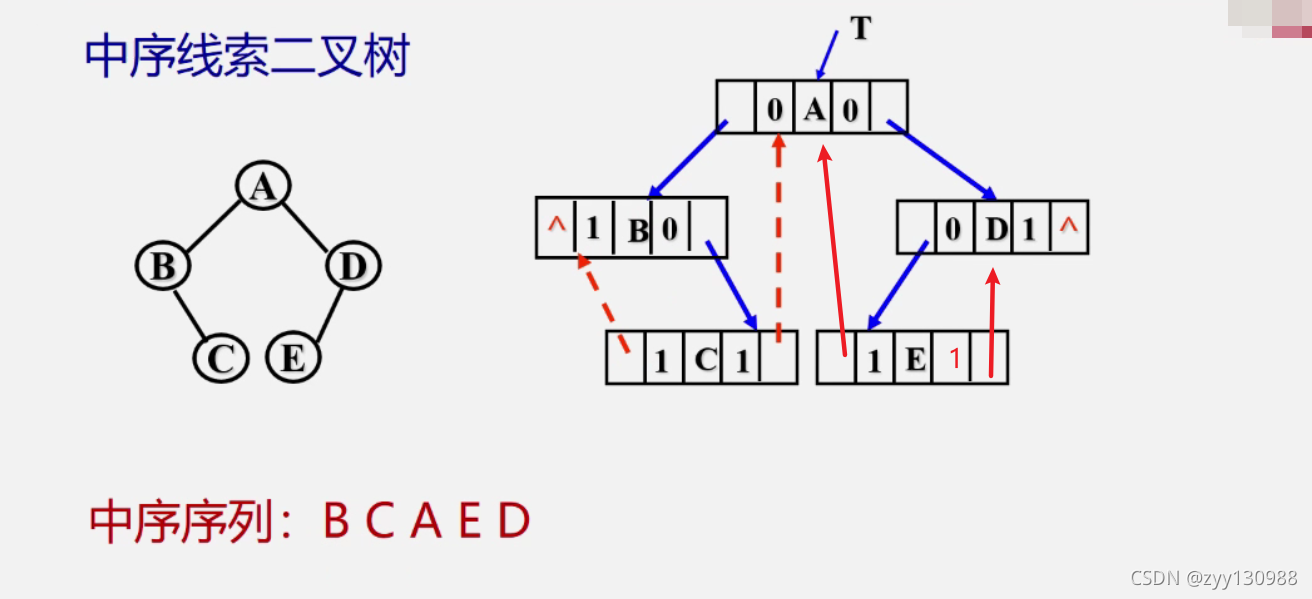
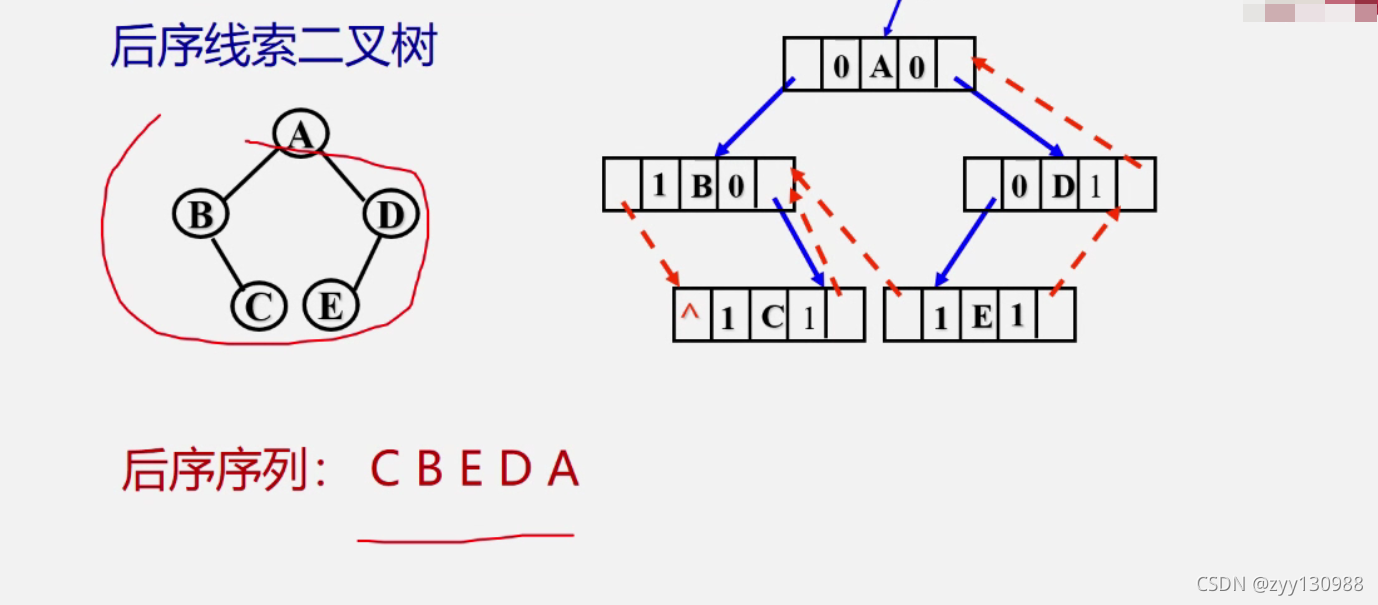
线索二叉树